Maximum Depth of N-ary Tree[Tree,Depth-First Search,Breadth-First Search]

https://leetcode.com/problems/maximum-depth-of-n-ary-tree/description/?envType=problem-list-v2&envId=tree

Given a n-ary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

 

Example 1:

Input: root = [1,null,3,2,4,null,5,6]
Output: 3

Example 2:

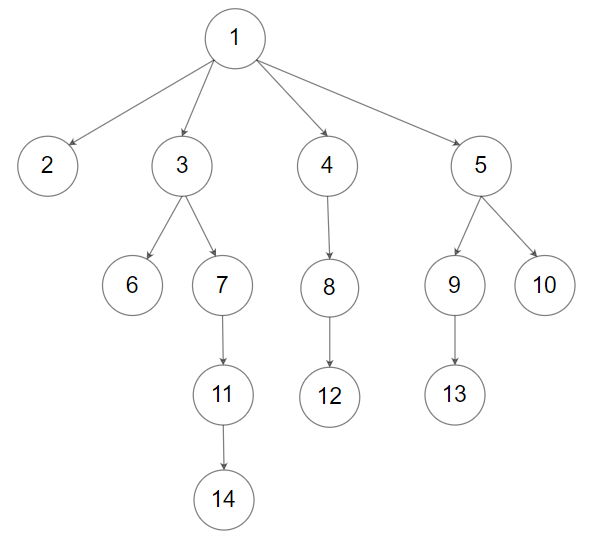
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: 5

 

Constraints:

• The total number of nodes is in the range [0, 104].
• The depth of the n-ary tree is less than or equal to 1000.

제목에서도 볼 수 있듯이 Recursive 또는 Stack/Queue + while문의 기운이 강하게 맴도는 녀석이다.

 

두려워 말고 진전해보자.

 

1. Python

Easy 난이도 이긴 하지만 ㅎㅎ...

일단 장하게도 별 도움 없이 Recursive하게 문제를 풀어냈다.

"""
# Definition for a Node.
class Node:
    def __init__(self, val: Optional[int] = None, children: Optional[List['Node']] = None):
        self.val = val
        self.children = children
"""

class Solution:
    def maxDepth(self, root: 'Node') -> int:
        # Make a stack of nodes
        # Increase cnt + 1 whenever it calls children
        
        # No.. go recursive
        if not root : return 0
        elif not root.children : return 1
        lst = deque()
        def helper(node,cnt):
            cnt+=1
            if not node.children :
                lst.append(cnt)
                return
            else :
                n = len(node.children)
                for j in range(n):
                    helper(node.children[j],cnt)

        for i in range(len(root.children)):
            cnt = 1
            helper(root.children[i],cnt)
        return max(lst)

아직 서툴러서 코드가 좀 조잡하다.

분명 같은 Recursive라도 좀 더 깔끔하게 코딩하는 방법이 있을 거 같기도 하다.

 

원래는 Stack, Queue를 써서 풀려고 했는데 머리가 굳어서 그렇게 할 수가 없었다..ㅠ

 

깔끔한 Recursive는 아래와 같다.

C를 이용해서 표현해 보았다

 

2. C

//  Definition for a Node.
struct Node {
      int val;
      int numChildren;
      struct Node** children;
 };
 

int max(int a, int b){
    return a >= b ? a : b;
}

int maxDepth(struct Node* root) {
    if(!root) return 0;

    int cnt = 0;
    for(int i=0;i<root->numChildren;i++){
        cnt = max(cnt,maxDepth(root->children[i]));
    }
    return cnt+1;
}

 

 

3. C++로는 Queue -> BFS , Stack -> DFS 모두를 해보자

 

3-1. Queue - BFS

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    int maxDepth(Node* root) {
        // BFS with Queue
        if(!root) return 0;

        queue<Node*> q;
        q.push(root);
        int cnt = 0;
        while(!q.empty()){
            int n = q.size();
            for(int i=0;i<n;i++){
                Node* curr = q.front();
                q.pop();
                for(auto x : curr->children) q.push(x);
            }
            cnt++;
        }
        return cnt;
    }
};

 

3-2. Stack - DFS

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    int maxDepth(Node* root) {
        int max_depth = 0;
        if(!root) return max_depth;

        stack<pair<Node*,int>> s;
        s.push({root,1});

        while(!s.empty()){
            Node* curr = s.top().first;
            int dept = s.top().second;
            s.pop();
            max_depth = max(max_depth,dept);
            for(auto x : curr->children){
                s.push({x,dept+1});
            }
        }
        return max_depth;
    }
};