https://leetcode.com/problems/is-graph-bipartite/description/?envType=problem-list-v2&envId=graph
There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:
- There are no self-edges (graph[u] does not contain u).
- There are no parallel edges (graph[u] does not contain duplicate values).
- If v is in graph[u], then u is in graph[v] (the graph is undirected).
- The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.
A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.
Return true if and only if it is bipartite.
Example 1:

Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.Example 2:
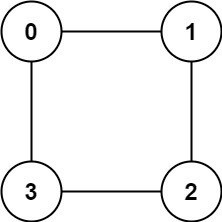
Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.
Constraints:
- graph.length == n
- 1 <= n <= 100
- 0 <= graph[u].length < n
- 0 <= graph[u][i] <= n - 1
- graph[u] does not contain u.
- All the values of graph[u] are unique.
- If graph[u] contains v, then graph[v] contains u.
일단 난이도는 medium의 문제다.
쫄지 말고 파헤쳐보자.
이놈의 graph 아오!
감이 잘 안 잡힌다. 대체 어떤 기준으로 set를 나눌 수 있는 것일까
1. Python
핵어려워서 결국 gpt를 봤다. 봐도 모르겄다 이거
세상엔 왜 이리 어려운 문제들이 많은 것인가 ㅠㅠ
class Solution:
def isBipartite(self, graph: List[List[int]]) -> bool:
n = len(graph)
colors = [-1] * n # -1로 초기화 (아직 색칠되지 않은 상태)
def dfs(node: int, color: int) -> bool:
colors[node] = color # 현재 노드를 주어진 색으로 색칠
for neighbor in graph[node]:
if colors[neighbor] == -1: # 이웃 노드가 색칠되지 않았다면
# 이웃 노드를 반대 색으로 색칠하고 DFS 재귀 호출
if not dfs(neighbor, 1 - color):
return False
elif colors[neighbor] == color: # 이웃 노드가 같은 색으로 칠해져 있다면
return False
return True
for i in range(n):
# 아직 색칠되지 않은 노드에 대해 DFS 실행
if colors[i] == -1:
if not dfs(i, 0): # 0부터 시작해서 색칠
return False
return True
뭐라는 거여.. 색칠을 왜하고, 색을 어떤 기준으로 칠하는거냐.. 하...
문제 이해그래프가 이분 그래프인지 확인하는 문제입니다. 이분 그래프란 모든 노드를 두 개의 그룹으로 나눌 수 있으며, 같은 그룹 내의 노드끼리는 연결되지 않은 그래프입니다.예를 들어, 한 그룹에 있는 노드는 색상 0으로, 다른 그룹은 색상 1로 색칠한다고 생각해보면, 서로 연결된 노드는 항상 다른 색이 되어야 합니다. 만약 연결된 두 노드가 같은 색이 되어야 하는 상황이 발생하면, 그 그래프는 이분 그래프가 아닙니다. 접근 방식 (DFS를 이용한 풀이)DFS (깊이 우선 탐색)를 사용하여 그래프의 각 노드를 방문하면서 두 그룹으로 나눌 수 있는지 확인하는 방식으로 풀 수 있습니다.
|
즉 independent 한 set A 와 set B의 각 Node들에 대해서 A / B 에 있는 Node가 서로 맞닿아 있으면 안 된다는 것이다.
아 진짜 문제 뭐같이도 만들었네. 무슨 퍼즐퀴즈하나 -_-
간만에 C로도 함 풀어보자
2. C
아오 거지 같은 거!
bool dfs(int** graph, int* color, int node, int col, int* graphColSize){
color[node] = col;
for(int k = 0; k<graphColSize[node]; k++){
int neighbor = graph[node][k];
if(color[neighbor]==-1){
if(!dfs(graph,color,neighbor,1-col,graphColSize))
return false;
}
else if(color[neighbor]==col) return false;
}
return true;
}
bool isBipartite(int** graph, int graphSize, int* graphColSize) {
int* color = (int*)malloc(graphSize*sizeof(int));
for(int i=0;i<graphSize;i++){
color[i] = -1;
}
for(int j=0;j<graphSize;j++){
if(color[j]==-1){
if(!dfs(graph,color,j,0,graphColSize)){
free(color);
return false;
}
}
}
free(color);
return true;
}
이번엔 자료구조를 이용해서 C++로도 풀어보자
class Solution {
public:
bool isBipartite(vector<vector<int>>& graph) {
int n = graph.size();
//Stack으로 풀어봅세
unordered_map<int,int> color;
for(int i=0;i<n;i++) color[i] = -1;
stack<pair<int,int>> node;
for(int j=0;j<n;j++){
if(color[j]==-1){
node.push({j,0});
while(!node.empty()){
int curr = node.top().first;
int col = node.top().second;
node.pop();
if(color[curr] == -1) color[curr] = col;
else if(color[curr] != col) return false;
for(int neighbor : graph[curr]){
if(color[neighbor]==col) return false;
else if(color[neighbor]==-1){
node.push({neighbor,1-col});
}
}
}
}
}
return true;
}
};
무식하게 꾸역꾸역 풀어보았다. 쉽지 않네;;
내친김에 python으로도 자료구조 함 풀어봐야지
-- Python
class Solution:
def isBipartite(self, graph: List[List[int]]) -> bool:
n = len(graph)
q = deque()
color = [-1]*n
for i in range(n):
if color[i]==-1:
q.append([i,0])
while q:
curr,col = q.pop()
if color[curr] == -1 :
color[curr] = col
elif color[curr] != col : return False
for neighbor in graph[curr]:
if color[neighbor] == col : return False
elif color[neighbor] == -1 :
q.append([neighbor,1-col])
return True여기서 q.append를 계속 color 0으로 해줄 수 있는 이유는,
이미 color[ i ] 가 색칠이 되어있지 않은 녀석은 '1'을 color로 가질 수 없다는 것이다.
예를 들어 0번째에서 이미 0과 adjecnt한 녀석은 1로 update 했기 때문에(0번째는 0으로 초기화 했었다) 그 다음 node들에 대해서 색이 칠해져 있다면 무조건 1로 칠해져 있을 것이고(0번째와 인접한 녀석들) 색이 안 칠해져 있다면 0으로 칠해야 하는 녀석이라 append는 계속 0으로 해주어야 한다.
이 과정이 계속 반복되다 보면, 색이 안 칠해져있는 녀석들에 대해선 0으로만 초기화 하면 되고 이미 칠해져 있는 녀석들은 색이 중간에 바뀌면 안 되니까 color[i] == -1에 걸리지 않고 넘어가게 되는 것이다.
이게 꼬이면 어떻게 하냐? 라고 질문한다면 그것이 while문에서 이미 return False가 뜨는 상황이다.
끝!