Find if Path Exists in Graph[Depth-First Search,Breadth-First Search,Union Find,Graph]

https://leetcode.com/problems/find-if-path-exists-in-graph/description/?envType=problem-list-v2&envId=graph

There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

You want to determine if there is a valid path that exists from vertex source to vertex destination.

Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise.

 

Example 1:

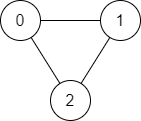
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2

Example 2:

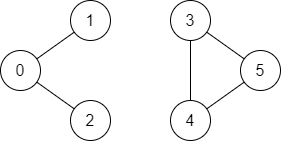
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.

 

Constraints:

• 1 <= n <= 2 * 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ui, vi <= n - 1
• ui != vi
• 0 <= source, destination <= n - 1
• There are no duplicate edges.
• There are no self edges.

Graph에서 Node를 Traversal하는 문제이다. 함 풀어보자.

 

좀 어려운 거 같은디..

 

1. Python

 

진한 recursive의 향기가 나서 해봤더만..

Time limit이 걸렸다.

아나 n을 30000으로 하면 우짜노 ㅠㅠㅠ

class Solution:
    def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        # feel like recursive..
        # find the source # make visited list with source node # check if destination node is in it
        visited = []
        def helper(node, edges):
            if node in visited : return
            visited.append(node)
            for edge in edges:
                if node in edge:
                    if edge[0] == node:
                        helper(edge[1],edges)
                    else : helper(edge[0],edges)
        helper(source,edges)
        if destination in visited:return True
        else : return False

일반적인 test case는 통과한다..

 

dict를 이용한 adjacent list를 만들라...!

class Solution:
    def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        # make adjacent list
        g = {i:[] for i in range(n)} #dictionary
        for u,v in edges:
            g[u] += [v]
            g[v] += [u]
        
        visited = set()

        # Recursive
        def helper(node):
            if node == destination: return True # 아..함수 안에 사용하면 바깥 함수 varialbe 사용가능하네
            visited.add(node)
            for neighbor in g[node]:
                if neighbor not in visited:
                    if helper(neighbor):
                        return True
            return False
        
        return helper(source)

 

2. C++

C++로도 한 번 풀어보자

 

이것은 queue로 고

class Solution {
public:
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        unordered_map<int,vector<int>> graph;
        for(auto vec : edges){
            graph[vec[0]].push_back(vec[1]);
            graph[vec[1]].push_back(vec[0]);
        }
        
        queue<int> q;
        unordered_set<int> visited;

        q.push(source);
        visited.insert(source);

        while(!q.empty()){
            int node = q.front();
            q.pop();
            if(node == destination) return true;

            for(int x : graph[node]){
                if(visited.find(x) == visited.end()){
                    visited.insert(x);
                    q.push(x);}
            }
        }
        return false;
    }
};

 

Recursive하게 풀거나 , while + queue 또는 while + stack 으로 문제를 푸는 것이다!

 

재귀적 DFS: helper 함수를 이용해 재귀적으로 탐색하는 방식입니다. 이 방식은 자연스럽게 스택 기반의 깊이 우선 탐색을 구현하게 되며, 코드는 간결해질 수 있지만, 그래프의 깊이가 깊을 경우 재귀 깊이 제한에 걸릴 수 있습니다. while + queue 또는 while + stack: while + queue (BFS): queue를 사용해 너비 우선 탐색(BFS)을 구현합니다. 이는 최단 경로를 찾거나, 목적지에 도달하는 데 최적화된 방식입니다. while + stack (iterative DFS): stack을 이용한 반복적 DFS는 재귀를 사용하지 않고 깊이 우선 탐색을 수행할 수 있는 방법입니다. 그래프 탐색에서 이 두 가지 방식은 거의 표준으로 사용되며, 특정 상황에 따라 적절히 선택할 수 있습니다.