Kth Smallest Element in a BST[Tree,Depth-First Search,Binary Search Tree,Binary Tree]

https://leetcode.com/problems/kth-smallest-element-in-a-bst/description/

Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.

 

Example 1:

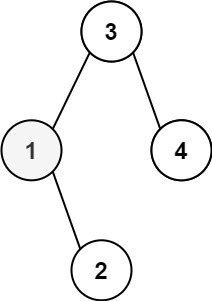
Input: root = [3,1,4,null,2], k = 1
Output: 1

Example 2:

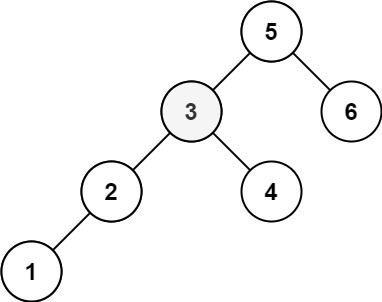
Input: root = [5,3,6,2,4,null,null,1], k = 3
Output: 3

 

Constraints:

• The number of nodes in the tree is n.
• 1 <= k <= n <= 104
• 0 <= Node.val <= 104

Follow up: If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize?

 

돌고 돌아 다시 leetcode BST문제이다.

 

In - order 느낌이 강하게 났다.

 

내가 이해한 Node Retrieval 문제는

Depth : Stack + while문 , 또는 Recursive

Breath : queue + while문이다.

 

1. Python

Stack + while문으로 풀어보았다.

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
from collections import deque
class Solution:
    def kthSmallest(self, root: TreeNode, k: int) -> int:
        #Traversal - In-Order?
        visited = []
        s = deque([root])
        while s:
            curr = s[-1]
            if curr.left and curr.left.val not in visited :
                s.append(curr.left)
                continue
            else :
                visited.append(curr.val)
                s.pop()
                if len(visited) == k : return visited[-1]
                if curr.right:
                    s.append(curr.right)

 

깊이 우선 탐색 (DFS): Stack + while: DFS는 스택과 while문을 통해 반복적으로 구현할 수 있습니다. 스택을 사용하여 노드를 계속 추적하며, 방문할 노드들을 저장합니다. Recursive: DFS는 재귀적으로도 쉽게 구현할 수 있습니다. 재귀 호출을 통해 자연스럽게 함수 호출 스택을 활용하여 노드를 깊이 우선으로 탐색합니다. 너비 우선 탐색 (BFS): Queue + while: BFS는 큐와 while문을 사용하여 반복적으로 구현하는 것이 일반적입니다. 큐를 통해 현재 레벨의 노드를 모두 방문하고, 다음 레벨로 이동합니다. Recursive: BFS는 재귀적으로 구현할 수 있지만, 구현 방식이 더 복잡합니다. 재귀적으로 하려면 각 레벨을 독립적으로 처리할 수 있도록 도와주는 별도의 자료구조나 함수를 만들어야 합니다. 이 방식은 일반적으로 **레벨 순회 (level-order traversal)**로 알려져 있으며, recursive BFS를 구현할 때는 보통 각 레벨에 대해 별도의 재귀 호출을 사용합니다.

 

위에 내가 푼 코드의 경우, GPT한테 개선점이 있는지 물어봤더니 visited라는 별도의 memory를 안 쓰고 푸는 방법을 알려주었다. 확실히 이렇게 하니까 가독성이 좀 더 좋긴 하다.. 아으

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        s = deque()
        curr = root
        cnt = 0
        while s or curr :
            while curr :
                s.append(curr)
                curr = curr.left

            curr = s.pop()
            cnt +=1
            if cnt == k : return curr.val

            curr = curr.right

 

 

2. C

이번엔 Recursive를 이용해서 풀어 본다.

//   Definition for a binary tree node.
struct TreeNode {
      int val;
      struct TreeNode *left;
      struct TreeNode *right;
};
 
void helper(struct TreeNode* node, int* cnt, int* result){
    if(!node) return;

    helper(node->left,cnt,result);

    (*cnt)--;
    if(*cnt==0){
        *result = node->val;
       return;
    }
    helper(node->right,cnt,result);

}

int kthSmallest(struct TreeNode* root, int k) {
    int result;
    helper(root,&k,&result);
    return result;
}

 

 

3.C++도 역시나 recursive하게!

//  * Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    void inorder(TreeNode* node, int& cnt, int& ans){
        if(!node) return;
        inorder(node->left,cnt,ans);
        cnt--;
        if(cnt==0){
            ans = node->val;
            return;
        }
        else inorder(node->right,cnt,ans);
    }
    int kthSmallest(TreeNode* root, int k) {
        int ans;
        inorder(root,k,ans);
        return ans;   
    }
};

 

 

참고로, Tree의 Traversal 순서에 따른 코드는 아래와 같다.

전위 순회 (Pre-order Traversal): 루트 -> 왼쪽 -> 오른쪽 중위 순회 (In-order Traversal): 왼쪽 -> 루트 -> 오른쪽 후위 순회 (Post-order Traversal): 왼쪽 -> 오른쪽 -> 루트

트리 노드 구조체 정의

#include <iostream>
using namespace std;

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

1. 전위 순회 (Pre-order Traversal)

void preorderTraversal(TreeNode* root) {
    if (root == nullptr) return;

    // 현재 노드 방문
    cout << root->val << " ";
    
    // 왼쪽 자식 방문
    preorderTraversal(root->left);
    
    // 오른쪽 자식 방문
    preorderTraversal(root->right);
}
2. 중위 순회 (In-order Traversal)

void inorderTraversal(TreeNode* root) {
    if (root == nullptr) return;

    // 왼쪽 자식 방문
    inorderTraversal(root->left);

    // 현재 노드 방문
    cout << root->val << " ";

    // 오른쪽 자식 방문
    inorderTraversal(root->right);
}
3. 후위 순회 (Post-order Traversal)

void postorderTraversal(TreeNode* root) {
    if (root == nullptr) return;

    // 왼쪽 자식 방문
    postorderTraversal(root->left);

    // 오른쪽 자식 방문
    postorderTraversal(root->right);

    // 현재 노드 방문
    cout << root->val << " ";
}

 

이상!