[Main course!] Review 7 - Inheritance in C++
https://eglife.tistory.com/89 Review 5 - Special Members in C++https://eglife.tistory.com/88 Review 4 - Class,Overloading,Special Members in C++https://eglife.tistory.com/87 Review 2 - Functions and Memory Management in C++https://eglife.tistory.com/85
eglife.tistory.com
이제 C++의 OOP를 위한 기본적인 공부는 끝이 났다.
이제 좀 Advanced한 영역인데, 슬~ 프로그래밍에 있어서 각종 알고리즘이 무엇이 있는지,
좀 더 고급화된 Data structure는 어떤 것이 있는지 확인해보자.
1. Data Structure

지금까지 배운 DS는 위와 같다.
Primitive DS엔 integer,float,Character,pointer 같은 기본 뼈대 친구들이 있고,
우리는 저기 Non-Primitive DS에 익숙해져야 한다.
특히, 지금 구현할 수 있는 프로그래밍언어가 Python, C, C++이 있는데, 각 언어로 Non-Primitive DS 구조를 만들 수 있어야 한다.
Python이야 기본적으로 제공하는 DS가 많아서 괜찮지만, C, C++로는 array / linked list를 이용해야 해서 쉽지 않을 것이다.
어쨌든, 계속해서 코딩을 해보며 Py,C,C++ 어떤 언어로도 저 Stack, Queue, Heap, Tree(BST,RED BLACK 등), Graph를 모두 구현할 수 있어야 하고 여기엔 Element Search/Insert/Delete Method도 구현되어 있어야 한다.
더 나아가 특정 DS에 대해서 Selection / Insertion / Merge Sort하는 알고리즘도 구현할 수 있어야 한다.
이렇듯 쉽지 않은 영역이다 코딩의 영역은..

단순한 DS들이 복잡한 DS들을 구현하기 위해 사용된다는 것이다.
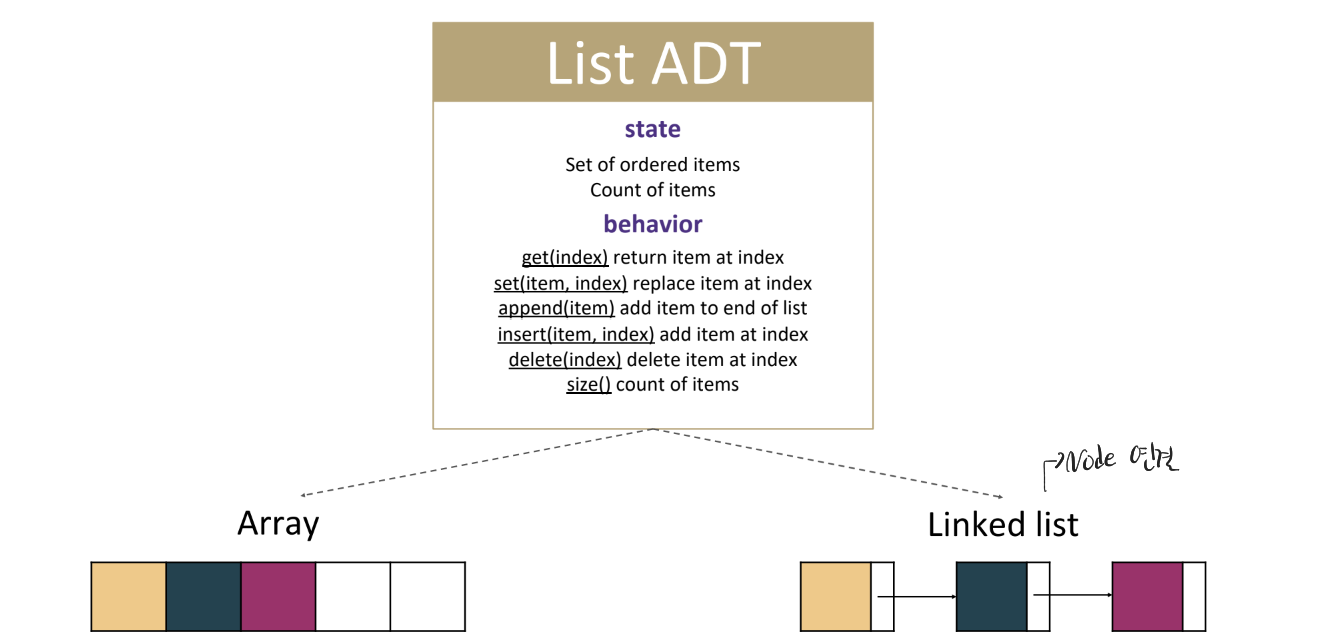
List의 경우도, 그 보다 하위 버전인 Array / Linked - list DS로 구현된 친구다.
한 DS를 구현하는 방법도 위와 같이 보통 여러 가지 case가 있는데, 각각의 장단점을 고려해서 적절한 코딩을 해줘야 한다.
ex : 위에서 array의 경우 element access는 편하지만 insert/delete에서 민족대이동을 해야해 시간소요가 크다.
반대로, Linked list의 경우 insert/delete는 편하지만, random access 할 때마다 O(N)의 시간소요가 걸린다.
이 밖에도 Robustness vs performance / reusability vs specific 등 다양하게 고려할 것들이 있다.

C++ Stack 구조를 한 번 예로 들어보자.
//void push(int), int pop(), int peek(), int isEmpty(), int size()
#include <iostream>
using namespace std;
class Stack{
public:
int *arr; // array도 이렇게 해준다.
int top;
int s;
int maxsize;
Stack(int m):s(0),top(NULL),maxsize(m){
arr = new int[m];
}
~Stack(){
delete[] arr;
}
void push(int a);
int pop();
int peek();
bool isEmpty();
int size();
};
void Stack::push(int a){
if( s >= maxsize){
cout << "FULL" <<endl;
return;
}
for(int i=1;i<=s;i++){
arr[i] = arr[i-1];
}
arr[0] = a;
s++;
}
int Stack::pop(){
if(isEmpty()) return -1;
int temp = arr[0];
for(int i=0;i<s;i++){
arr[i]=arr[i+1];
}
s--;
return temp;
}
int Stack::peek(){
if(isEmpty()) return -1;
return arr[0];
}
bool Stack::isEmpty(){
return s==0;
}
int Stack::size(){
return s;
}
int main(){
Stack s(10);
cout << s.peek() << " " << s.isEmpty() << " "<< s.size() <<endl;
s.pop();
cout << s.peek() << " " << s.isEmpty() << " "<< s.size() <<endl;
s.push(1);
s.push(3);
s.push(5);
s.push(7);
s.pop();
cout << s.peek() << " " << s.isEmpty() << " "<< s.size() <<endl;
s.push(9);
cout << s.peek() << " " << s.isEmpty() << " "<< s.size() <<endl;
return 0;
}
이렇게 짜봤는데, 코드는 잘 돌아가지만
정석 답은 아니었다.
정석은 array의 경우 그냥 top 이라는 index로 조절해가며 method를 구현하는 것 like below
//void push(int), int pop(), int peek(), int isEmpty(), int size()
#include <iostream>
using namespace std;
class Stack{
public:
int *arr; // array도 이렇게 해준다.
int top;
int maxsize;
Stack(int m):top(0),maxsize(m){
arr = new int[m];
}
~Stack(){
delete[] arr;
}
void push(int a);
void pop();
int peek();
bool isEmpty();
int size();
};
void Stack::push(int a){
if(top >= maxsize){
cout << "FULL" <<endl;
return;
}
arr[top] = a;
top++;
}
void Stack::pop(){
if(isEmpty()) return;
top--;
}
int Stack::peek(){
if(isEmpty()) return -1;
return arr[top-1];
}
bool Stack::isEmpty(){
return top==0;
}
int Stack::size(){
return top;
}
int main(){
Stack s(10);
cout << s.peek() << " " << s.isEmpty() << " "<< s.size() <<endl;
s.pop();
cout << s.peek() << " " << s.isEmpty() << " "<< s.size() <<endl;
s.push(1);
s.push(3);
s.push(5);
s.push(7);
s.pop();
cout << s.peek() << " " << s.isEmpty() << " "<< s.size() <<endl;
s.push(9);
cout << s.peek() << " " << s.isEmpty() << " "<< s.size() <<endl;
return 0;
}
이번엔 Linked List로 구현을 함 해보자
#include <iostream>
using namespace std;
struct Node{
int data;
Node* next;
Node(int x):data(x),next(nullptr){}
};
class Stack{
public:
Node *head;
int s;
Stack():head(nullptr),s(0){}
~Stack(){
while(!isEmpty()){
pop();
}
}
void push(int x);
void pop();
int peek();
bool isEmpty();
int size();
void print();
};
void Stack::push(int x){
Node *newNode = new Node(x);
if(isEmpty()){
head = newNode;
s++;
return;
}
newNode -> next = head;
head = newNode;
s++;
}
bool Stack::isEmpty(){
return s==0;
}
void Stack::pop(){
if(isEmpty()) return;
Node* temp = head;
head = head->next;
delete temp;
s--;
}
int Stack::peek(){
if(isEmpty()) return -1;
return head->data;
}
int Stack::size(){
return s;
}
void Stack::print(){
if(isEmpty()) return;
Node*temp = head;
while(temp){
cout << temp->data << " ";
temp = temp->next;
}
cout << "SIZE: " << s <<endl;
}
int main(){
Stack test;
Stack* S = &test;
S->pop();
S->print();
S->push(10);
S->push(15);
S->push(1);
S->push(13);
S->print();
S->pop();
S->print();
S->push(111);
S->pop();
S->push(-11);
S->print();
// 13 1 15 10 SIZE: 4
// 1 15 10 SIZE: 3
// -11 1 15 10 SIZE: 4
return 0;
}
2. Priority Queues

원래 기본 queue는 FIFO라 중간 element에 접근할 일이 없어서 indices가 무의미했다.
근데 PQ는 각 element마다 priority를 가지고 있어서, Enqueue / Dequeue시 이 priority 기준으로 저장되고 POP된다.
구현할 수 있는 방식은 아래와 같이 여러 가지가 있다.
 |
 |
※ 코딩테스트를 위해선 이 잡다한 걸로도 PQ를 다 구현할 수 있어야 한다.
3. Heap
이런 Priority 구조를 가장 잘 표현할 수 있는 DS가 바로 Heap이다.

이 Heap에는 따져줘야 할 것들이 좀 있다
- Structured Property : Completeness
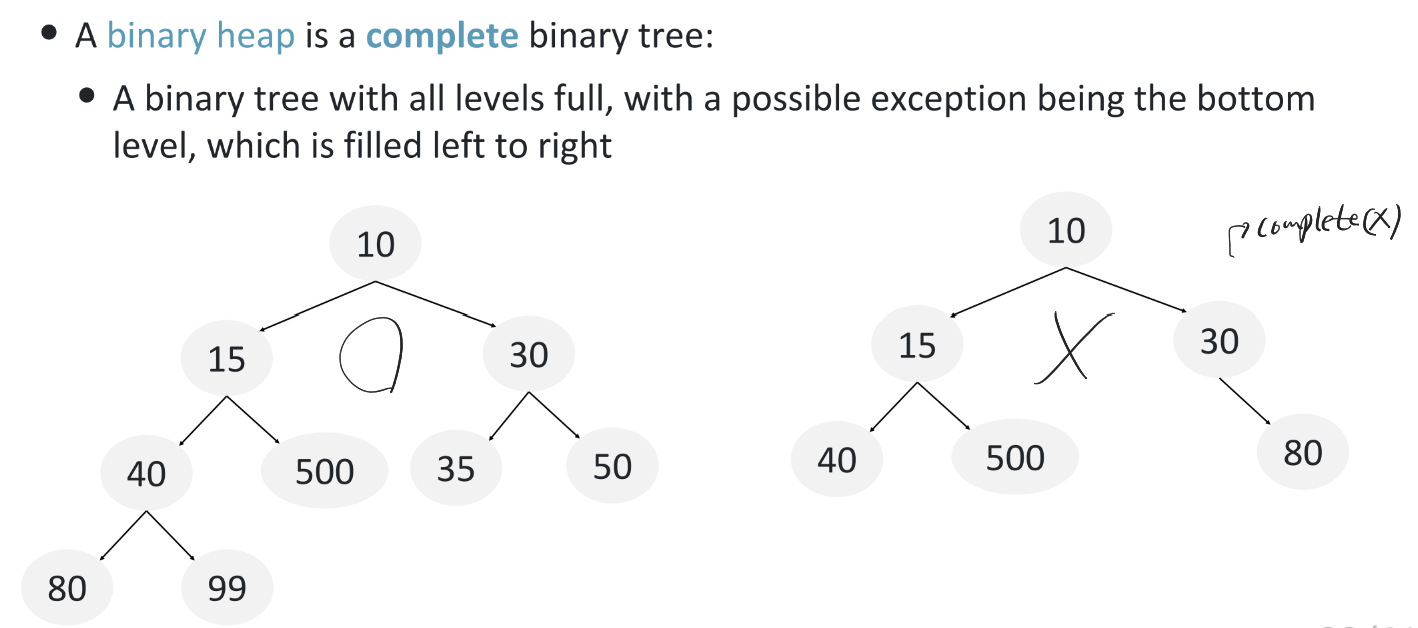
항상 tree는 왼쪽부터 오른쪽 방향으로 순서대로 FULLY 채워나가야 한다.
- Heap Propery ( 요건 MIN-Haep 기준 )

즉 Heap(정확히는 Binary Min heap)의 경우엔 구조는 Complete Binary Tree이고 모든 부모는 자식보다 크기가 작아야 한다는 Heap Property를 만족해야 한다.
Heap의 경우 통상 Height는 log(N) 이고 이놈으로 Priority Queue를 만들곤 한다.
근데, 이 Struct / Heap Property 때문에 Data를 넣고 뺄 때마다 Recovery가 필요하다. ㅠㅠ
일단 element 추가 or 제거 후에 Structure 부터 살피고, 그 다음 Heap Property를 복구한다.

Insert / Delete 모두 O(log N)이 소요된다.
PQ는 Heap 말고 Array로도 구현할 수 있는데, Array 구조 특성때문에 Structure를 고려하지 않아도 되어 method 구현이 쉬운 편이다.


PQ를 haep으로도 해보고, array로도 한 번 구현해보자! 필수 필수!
hint:

-E. O. D-
'SW 만학도 > C++ & Algorithm' 카테고리의 다른 글
| Review 10 - Single-Source-Shortest Path in C++ (0) | 2024.08.02 |
|---|---|
| Review 9 - MST(Minimum Spanning Trees) in C++ (8) | 2024.07.24 |
| [Main course!] Review 7 - Inheritance in C++ (0) | 2024.07.21 |
| Review 5 - Special Members in C++ (0) | 2024.07.20 |
| Review 4 - Class,Overloading,Special Members in C++ (1) | 2024.07.19 |