[Algorithm] Review 8 - Priority Queues and Heaps in C++
https://eglife.tistory.com/92 [Main course!] Review 7 - Inheritance in C++https://eglife.tistory.com/89 Review 5 - Special Members in C++https://eglife.tistory.com/88 Review 4 - Class,Overloading,Special Members in C++https://eglife.tistory.com/87 Revi
eglife.tistory.com
본격적으로 알고리즘의 세계에 발을 디뎠다.
1. Graph
이 장을 포함해, 앞으로 가장 많이 다루어질 Data Structure는 Graph다.
모~든 DS를 표현할 수 있는 DS로서 가장 Flexable한 친구다.
기본적으로 Node(Vertices, Element)와 그 Node 사이를 이어주는 Edge로 구성이 되어있다.
Graph 관련 용어들을 일차적으로 먼저 정리해보겠다.
- Undirected Graph : edge의 방향성이 없는 Case다. 서로 이어진 Node들은 양방향 통행 가능
- Directed Graph : 일방향
- Degree : 해당 Vertex에 이어진 edge의 개수
- Path : Vertex간 이어진 경로인데, 중간에 Vertex방문 중복이 없다.
- Reachable : Vertex간 서로 path가 있으면 서로 reachable하다.
- Complete : 모든 Vertices가 서로 direct edge로 이어여 있는 경우
- Cycle : Path의 시작 / 끝 Node가 같은 경우
- Acyclic Graph : Cycle이 없는 Graph다.
- Loop : In/Out 이 self인 Edge
- Simple Graph : self - loop / parallel edge가 없는 graph다. 즉 Vertex간 Edge가 Unique하게 표현되는 경우
어떤 Edge는 Weight을 가질 수 있어서 edge끼리 서로 구별될 수 있다. 이러한 경우를 Weighted Graph라고 한다.
Graph와 Tree의 차이점이 뭘까? 일단 포함관계로 Graph가 압승이다. 즉, 모든 Tree는 graph이다.
다만 Tree는 acyclic이라는 점에서 graph의 부분집합이다.
2. Representing Graphs
Graph를 표현하는 방법엔 뭐가 있을까?
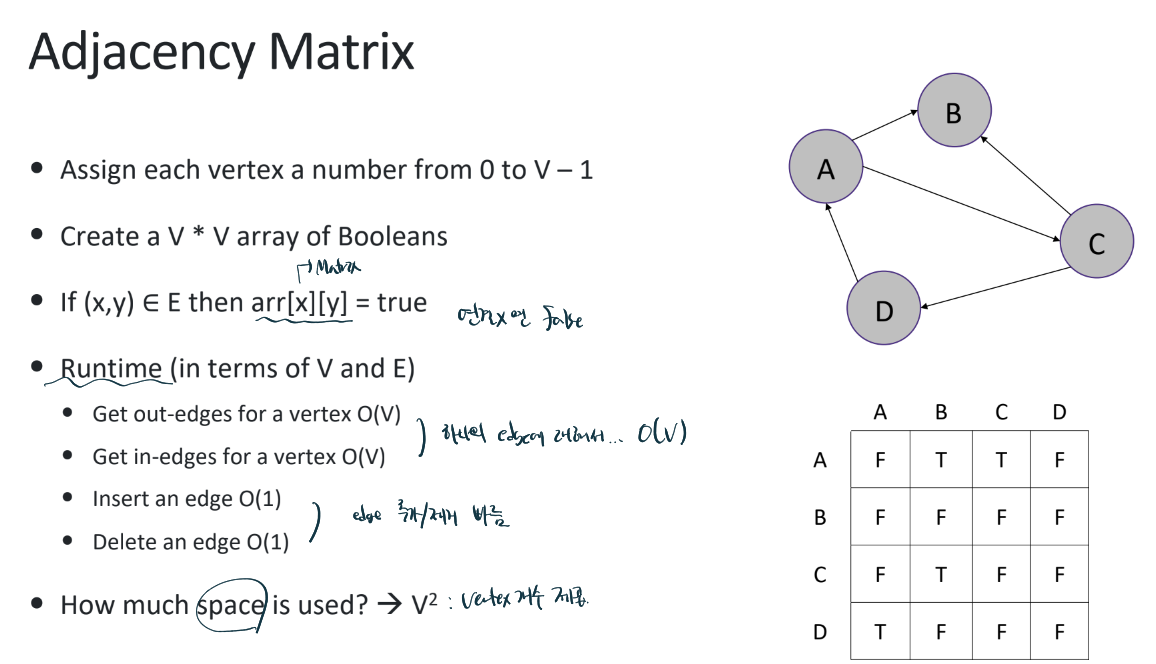
- Adjacency list / Matrix
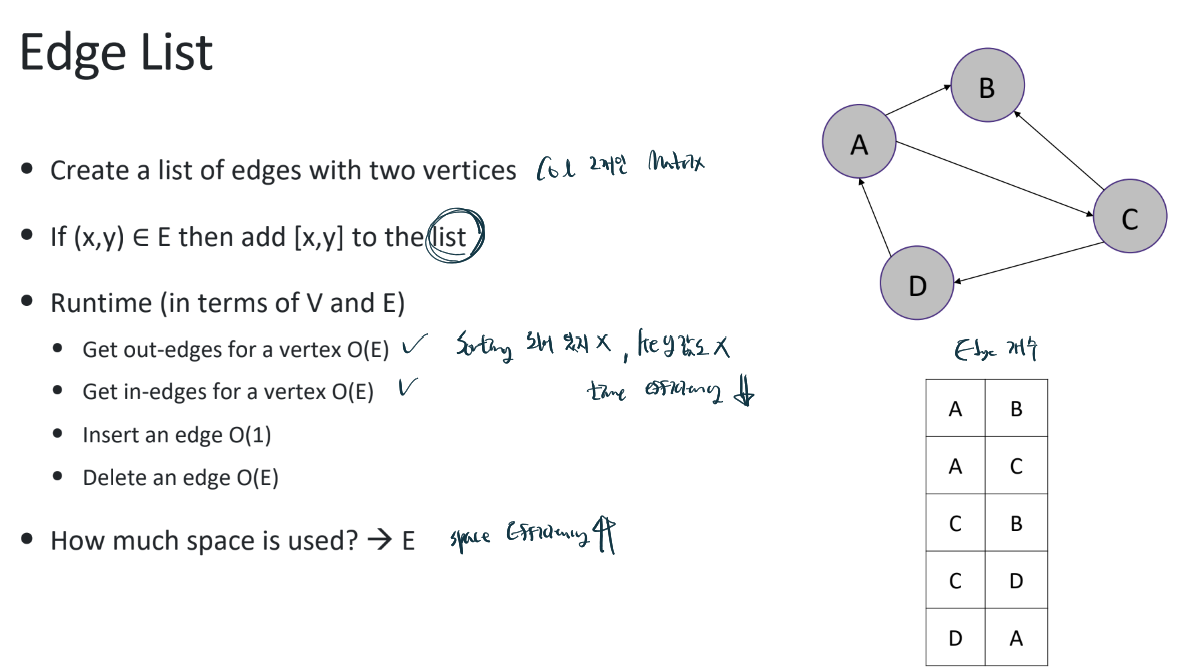
- Edge list
요렇게 2가지 Case가 기본적으로 많이 쓰이는 방법이다.
일단 전자의 경우, Edge보다 Vertex수가 압도적으로 많으면 보통 list를 쓴다.
즉, Graph가 Sparse(V 多) 하면 list , Dense하면 Matrix (V 少) 를 쓴다.
만약, Vertex정보가 별로 필요 없는 경우라면 그냥 Edge list를 쓴다.

3. Graph Traversal
기본적으로 Breadth First Search와 Depth First Search가 있으며, BFS의 경우 보통 Queue 구조를 많이 쓴다.(FIFO)
반대로 DFS의 경우엔 Stack 구조를 구현다는 데 많이 쓴다.(LIFO)
#include <iostream>
#include <list>
#include <vector>
#include <queue>
#include <stack>
#include <algorithm>
using namespace std;
class Graph {
public:
Graph(int V); // Constructor
void addEdge(int v, int w); // function to add an edge to graph
void DFS(int v); // DFS traversal from a given vertex v
void BFS(int v); // BFS traversal from a given vertex v
private:
int V; // No. of vertices
std::list<int> *adj; // Pointer to an array containing adjacency lists
void DFSUtil(int v, std::vector<bool> &visited); // A function used by DFS
};
// Constructor
Graph::Graph(int V) {
this->V = V;
adj = new std::list<int>[V];
}
// Function to add an edge into the graph
void Graph::addEdge(int v, int w) {
adj[v].push_back(w); // Add w to v’s list.
adj[w].push_back(v); // Add v to w’s list.
}
// A function used by DFS
void Graph::DFSUtil(int v, std::vector<bool> &visited) {
// Mark the current node as visited and print it
stack<int> s;
s.push(v);
while(!s.empty()){
int temp = s.top();
s.pop();
if(visited[temp]==false){
visited[temp] = true;
cout << temp << " ";
}
for(int x : adj[temp]){
if(visited[x]==false){
s.push(x);
}
}
}
}
// DFS traversal of the vertices reachable from v
void Graph::DFS(int v) {
vector<bool> visited(V,false);
DFSUtil(v,visited);
}
// BFS traversal of the vertices reachable from v
void Graph::BFS(int v) {
queue<int> q;
vector<bool> visited(V,false);
q.push(v);
while(!q.empty()){
int temp = q.front();
q.pop();
if(visited[temp]==false){
visited[temp]=true;
cout << temp << " ";
}
for(int& n : adj[temp]){
if(visited[n]==false){
q.push(n);
}
}
}
}
// Main function to test the graph traversal methods
int main() {
// Create a graph given in the above diagram
Graph g(5); // 5 vertices numbered from 0 to 4
g.addEdge(0, 1);
g.addEdge(0, 4);
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(1, 4);
g.addEdge(2, 3);
g.addEdge(3, 4);
std::cout << "Depth First Traversal (starting from vertex 0):\n";
g.DFS(0);
std::cout << "\nBreadth First Traversal (starting from vertex 0):\n";
g.BFS(0);
return 0;
}
Depth First Traversal (starting from vertex 0):
0 4 3 2 1
Breadth First Traversal (starting from vertex 0):
0 1 4 2 3
Depth First Traversal (starting from vertex 1):
1 4 3 2 0
Breadth First Traversal (starting from vertex 1):
1 0 2 3 4
한 번 코딩을 해봤다 대햇
4. Minimum Spanning Trees
MST란, 간단히 말해서 모든 Node를 포함하는 path 중 가장 cost가 적은 것을 말한다.
Node끼리 연결하는 Spanning Tree는 많은데, 그 중 cost가 가장 적은 친구가 MST!


주어진 Graph에서 MST를 찾을 땐, 일단 Spanning Tree를(Acyclic + 모든 Node 연결) 만들 때까지 edge를 하나씩 추가해 나간다.
이 때, 추가된 edge가 safe하냐를 check하는 것이 관건이다! safe하다는 것은 이놈을 추가했을 때 최종적인 MST형태가 만들어지냐는 것!

이 때 사용되는 Theorem이 바로 위 정리다.
그냥 edge를 더해 나갈 때, u or v에 연결된 light edge를 더해나가도 이 놈이 최종 MST의 subset이라는 것이다.
이 내용을 바탕으로 MST를 만드는 2가지 알고리즘이 바로
- Prims Algorithm
- Kruskal Algorithm
얘네는 기본적으로 현 시점 최선의 선택을 하는 #Greedy_Algorithm이다.

Prims는 Vertex 기반으로 가장 작은 edge를 추가해나가고, Kruskal은 edge들 중에 cycle을 만들지 않는 작은 edge들을 추가해나간다. 즉 얘는 좀 edge기반!
5. Prim's Algorithm

기본적으로 Priority Queue data structure를 사용하며,
일단 모든 Node 들의 cost를 INF로 두고, unmark 한다.
그리고 node V에서 Search 시작을 하는데, 첫 cost[V]는 0, prev[V]도 0으로 둔다.
그 다음 새로운 연결 node U를 찾으면 그 놈의 cost를 U<->V의 cost로 update 하고 Mark를 한다.

대략적인 알고리즘 진행절차는 위와 같다.
6. Kruskal Algorithm
Kruskal역시 Priority queue를 사용한다. Kruskal에 사용될 기본적인 Structure는 아래와 같다.

x라는 Node가 있는 Set을 만드는 Make / 그리고 새로운 Node y를 이 set에 포함시키는 Union / 그리고 특정 node 를 가리키는 Find가 있다.

Kruskal 알고리즘의 수도코드이다.
weigth이 작은 Edge부터 set A에 하나씩 추가시키는데, weigth이 작은 놈은 priority queue의 특성으로 골라내고 set A에 추가시킬 때는 circle이 생기지 않게 Find-Set을 통해 추가시키려는 친구가 이미 SET에 있는지 확인부터 한다.
Kruskal MST가 갖는 Edge의 수는 Node-1개이다. 즉 N-1개의 Edge가 accept되는 순간 더 이상 MST의 변화는 없다.

- E. O. D -
'SW 만학도 > C++ & Algorithm' 카테고리의 다른 글
| Review 11 - Dynamic Programming (0) | 2024.08.03 |
|---|---|
| Review 10 - Single-Source-Shortest Path in C++ (0) | 2024.08.02 |
| [Algorithm] Review 8 - Priority Queues and Heaps in C++ (3) | 2024.07.22 |
| [Main course!] Review 7 - Inheritance in C++ (0) | 2024.07.21 |
| Review 5 - Special Members in C++ (0) | 2024.07.20 |