Review 9 - Queues & Stacks
https://eglife.tistory.com/77 Review 8 - Python Data Structurehttps://eglife.tistory.com/75 Review 7 - Python Algorithm design & Testing & Debugginghttps://eglife.tistory.com/74 Review 6 - Python Recursion & Merge Sorthttps://eglife.tistory.com/73 Revi
eglife.tistory.com
끝을 향해 달려가는 Python Review
사실상 이 Chapter에서 다룰 내용을 다루기 위해 지금껏 복습해왔다고 해도 과언이 아니다.
그만큼 각종 퀴즈, 시험 같은 것에 주로 나오는 것이 여러 Tree, Graph 구조 of Python이다.
이것들은 Python 외에도 C, C++ 로도 코드를 짜야할 경우가 많으니 가장 강도 높은 집중도가 요구된다.
차근 차근 밟아 나가보자.
1. Binary Search Tree

Linked List의 단점에서 착안된 개념이다.
Array와 달리 Linked List는 Element를 Search하는데 시간이 너무 오래 걸린다.
First가 항상 맨 앞이라 데이터를 찾으면 O(N)이기 때문이지요
First가 만약 중앙쪽이라면 시간을 1/2 정도로 관리 가능하겠지만, Big O 차원에선 여전히 O(N)이다.
그래서 이 때, Binary Search 기법을 사용하면 시간을 줄일 수 있고, 그 때 필요한 모형이 Tree 모양이다.
Tree 는 Cycle이 있으면 안 된다.
Tree의 조건
1) Node들 간 연결되어 있던가, Node가 하나뿐이다.
2) 한 Node에서 다른 Node로 가는 Path는 하나뿐이다.
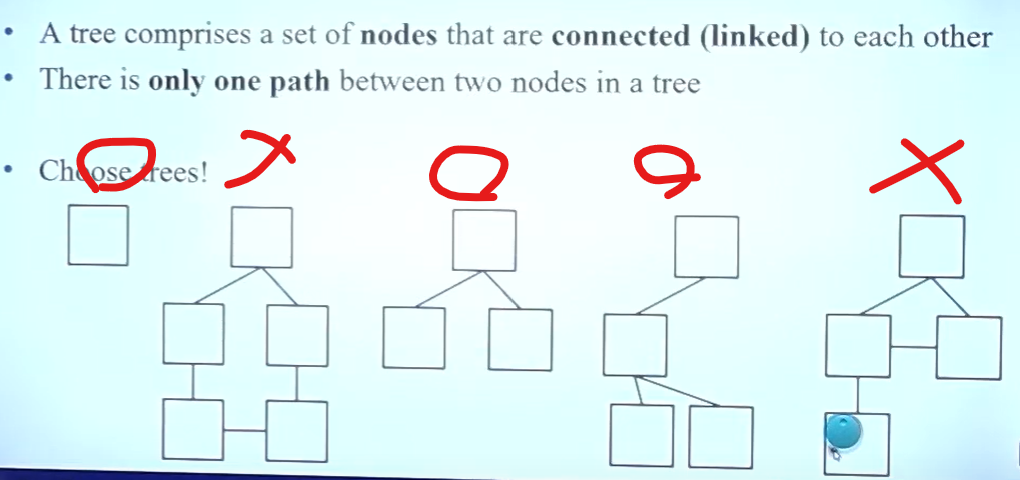
Rooted Tree란? : Root가 하나인 Tree다.( Tree의 맨 위에 위치 ), 그리고 Chile Node는 부모 Node가 하나다. Chile가 없는 Node는 leaf라고 한다.
Rooted Binary Tree는 : Rooted Tree에서 자녀를 최대 2개 가질 수 있다.
Binary Search Tree는 : Rooted Binary Tree에서 조건을 추가한다.

통상 BST에는 Search / Insert / Delete 3가지 Method를 제공해야 하는데, 각 영역에 대해서 알아보자
a. Search :
class TreeNode:
def __init__(self,x:int):
self.val = x
self.left = None
self.right = None
class BST():
def __init__(self):
self.root = None
def searchHelp(curNode:TreeNode,x:int) -> TreeNode:
# Base Case
if not curNode : return None
# Recursive Case
if x == curNode.val :
return curNode
elif x > curNode.val :
return searchHelp(curNode.right,x)
else :
return searchHelp(curNode.left,x)
def search(self, x:int)->TreeNode:
return self.searchHelp(self.root,x)
요렇게 Recursive하게 진행한다.
b. Insert :
def insertHelp(curNode:TreeNode,x:int)->TreeNode:
#Base Case
if not curNode:
return TreeNode(x)
#Recursive
if x < curNode.val:
curNode.left = self.insertHelp(curNode.left,x)
elif x > curNode.val:
curNode.lright = self.insertHelp(curNode.right,x)
else :
return curNode
def insert(self, x:int)->None:
self.root = self.insertHelp(self.root,x)
코드를 잘 따라가보자.
c. Delete : 끝판왕
여러가지 Case가 있다. 모든 case를 잘 고려하자
Case 1 : 자녀 X Node 제거 , Case 2 : 자녀 1 Node 제거 , Case 3 : 자녀 2 Node 제거
Case 1 -> 그냥 제거
Case 2 -> 내가 제거 되면서 내 부모랑 자식 연결해주기
Case 3 -> 내가 제거 되면서 나의 왼편에서 가장 오른쪽 친구 or 나의 오른편에서 가장 왼쪽 친구를 내 자리에 두기
이 때, 그 친구가 빠지면서 똑같이 Delete Case를 적용시킨다.
BST가 Balanced 구조라면, Search 하는 Time은 O( log N ) 이다. 근데, Balanced 되어있지 않고 Linked List처럼 일열로 쭉 늘어진 경우 O(N)이라서 Tree에 Insert 할 때, Balanced 구조를 잘 지켜질 수 있도록 해야한다.
def delete(self, x: int) -> None:
def deleteHelp(curNode: TreeNode, x: int) -> TreeNode:
if not curNode:
return None
if x < curNode.val:
curNode.left = deleteHelp(curNode.left, x)
elif x > curNode.val:
curNode.right = deleteHelp(curNode.right, x)
else:
if not curNode.left:
return curNode.right
if not curNode.right:
return curNode.left
temp = self.findMin(curNode.right)
curNode.val = temp.val
curNode.right = deleteHelp(curNode.right, temp.val)
return curNode
self.root = deleteHelp(self.root, x)
def findMin(self, curNode: TreeNode) -> TreeNode:
while curNode.left is not None:
curNode = curNode.left
return curNode
BST의 Search , Insert , Delete 다 Practice 해보기!
2. Trees and Traversals
우리 일상에 있는 여러 Data는 사실 tree구조로 되어 있는 것이 많다.
그래서 Tree structure을 배우고, 쓰는 것이다.
일반적인 tree는 꼭 2개의 child가 있을 건 아니다. K-ary tree -> 자식을 K개씩 가질 수 있다.

3. Breadh - First ( Level - Order ) Traversal
Tree구조를 가로줄로 쭉쭉 순서대로 방문한다.
class Tree():
def visit(self, node: TreeNode):
print(node.val)
def BFT(self):
if self.root == None:
return
q = [self.root]
while q:
curNode = q.pop(0)
self.visit(curNode)
for childNode in curNode.child:
if childNode:
q.append(childNode)
BFT는 Queue를 쓴다. q 라는 list를 만들었는데, 이게 우리가 알고있는 #queues 구조라고 생각하면 된다.
visit 함수를 거쳐야 print가 되는 구조다. 위와 같이 짜면 queues의 특성으로 우리가 BFT를 할 수 있을 지 시뮬레이션을 돌려보자.
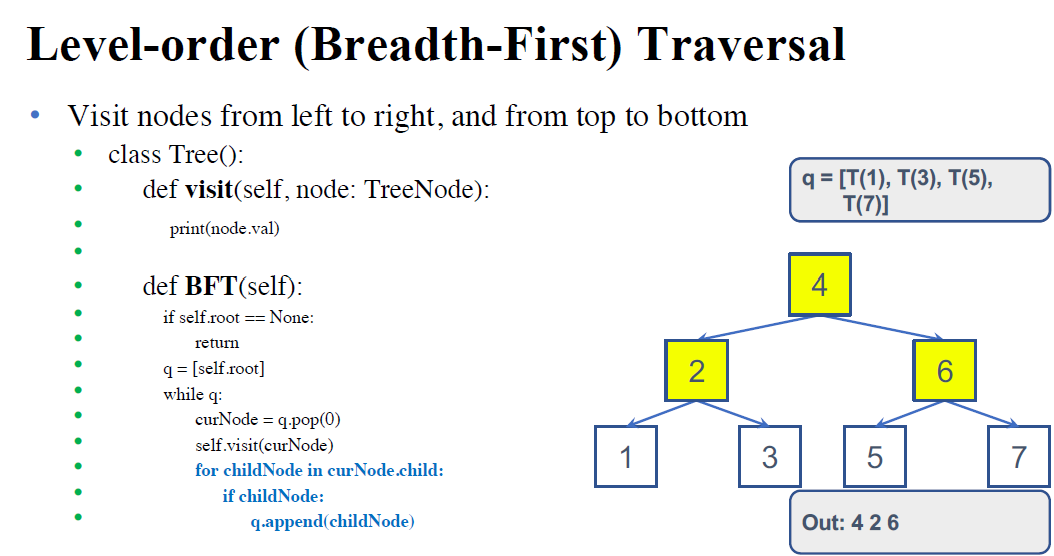
모든 Tree의 Node를 전부 왼->오 순으로 방문할 수밖에 없는 Powerful한 알고리즘이다.

Python에선 Doubly-linked list인 deque(import 해야함) 구조를 제공해서 BFT를 좀 더 빨리 구 할 수 있다.
4. Depth - First Traversal ( 아까는 횡으로, 이번엔 밑으로 먼저 깊게 파보자 )
- 3가지 Case가 있다. (1. Preorder 2.Inorder 3. Postorder )
- 이 3가지는 코드는 비슷한데, Visit을 언제하냐의 차이다.
BFT는 Loop 형식이었는데, 기본적으로 DFT는 Recursion을 사용한다.

Preorder의 경우 Directory List를 불러올 때, 상위 폴더-> 하위 폴더 -> 하위 폴더 이런 구조를 만드는 경우에 쓰인다.
Inorder의 경우 가장 왼쪽 밑을 찍었을 때 처음으로 Output이 Print에 찍힌다.
Why inorder인가? Visit하는 숫자가 1씩 증가한다. 1.2.3....

이거 어따 쓸까? Binary Search Tree를 우리가 만들었다고 가정했을 때, 얘를 그냥 Flatten 해서 list로 만들고 싶다면 DFT를 Inorder로 돌리면 1,2,3,4.. 이렇게 쫙 펴진 값을 얻을 수 있다.

Postorder는 내 자녀를 다 방문하고 나서야 '나'를 방문하는 것이다.
이런 건 전체 file 사이즈를 구할 때 유용하다. 밑에서부터 하나씩 긁어오면서 size를 더해가면 된다.

이런 거 외에도, Database에서 B-Tree, B+ tree를 배울텐데 그건 그 때가서 열심히 공부하자..
Summary :
BFT = FIFO (Python에선 Deque)
DFT = LOOP를 써서도 구현할 수 있다. LIFO Stack을 사용하고 Python에선 역시 Deque를 사용하면 되는데, 추천하진 않는다. 차라리 Recursion으로 구현하는 것이 더 낫다는 뜻.
그리고 DFT엔 Pre/In/Postorder 이렇게 3가지의 방문 방법이 있다.
5. Graph and Traversal
Tree는 계층적인 구조, Hierarchy가 있을 때 그것을 표현하기에 적절한 구조이다.
지하철 노선도 같이 Node들이 1 way가 아니고 여러 경로로 연결된 경우 Tree로 표현 못 한다. 그래서 우리는 Graph 개념을 도입한다.
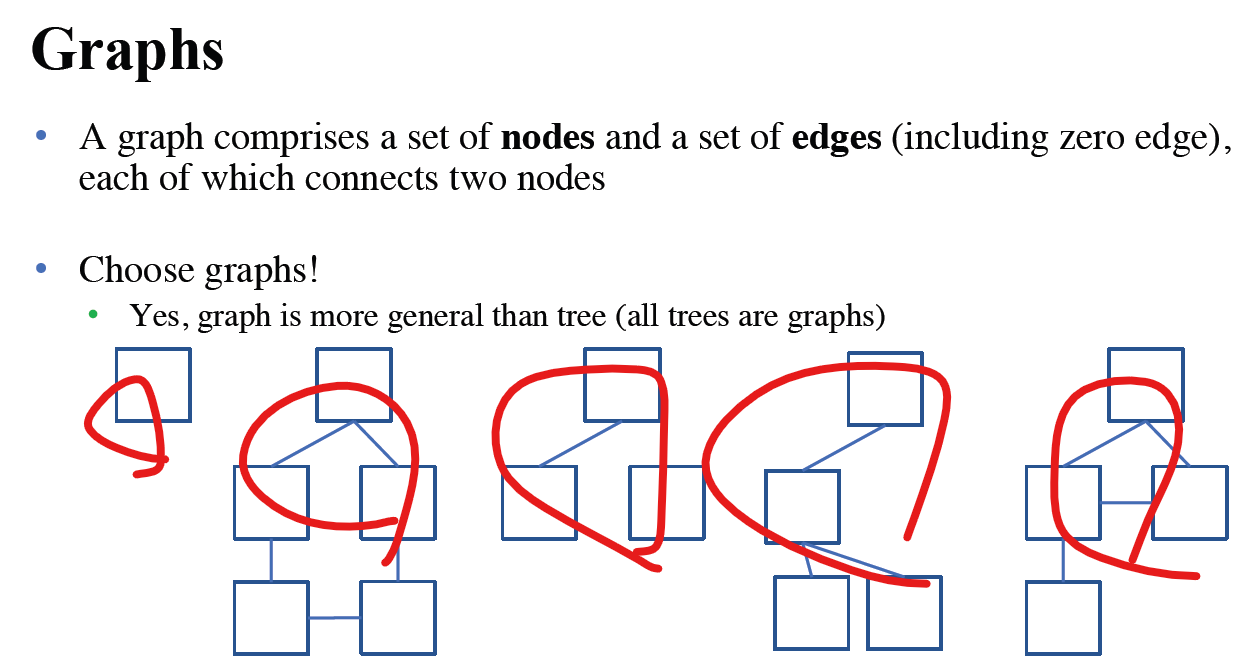
Node와 Edge가 있기만 하면 모두 Graph다.
보다시피 Graph는 굉장히 Broad한 개념이다. 어지간하면 Graph이고 Tree보단 당연히 General 한 structure이다.
Graph는 너무 종류가 다양해서, 우리는 Simple Graph만 고려하기로 한다.
Simple Graph? : 1. Loop이 없다.(edge (v,v)가 없다.) 2. Parallel Edge가 없다.( e1(v,w) / e2(v,w) 이렇게 2개가 있지 않다.)
2개의 Node(Vertex)가 서로 연결되어 있다면 adjacent 하다고 한다. Path는 Node 간 연결 선인 edge가 특정 vertext에서 특정 vertex까지 연결되어 있으면 그 전체경로를 path라고 한다. Path 중간에 같은 vertex가 2번 나오면 Simple하지 않는다. 즉, Simple Path는 Cycle이 없는 path다. Graph인데 cycle이 있으면 cylic graph, cylce이 없으면 acyclic graph라고 부른다. 어떤 두 vertex가 연결되어 있으면 connected라고 한다.
※ Loop은 cycle의 일종이다. Loop은 바로 나->나 이고, cycle은 돌고 돌아 나에게로 돌아오는 것이다.
edge는 두 종류가 있다. 1. 방향성 X : undirected , 2. 방향성 O : directed(like an Arrow) -> 이 때는 일방통행이다.
graph with undirected edges : undirected graph <-> directed graph

list 값 자체가 수정되면 안 되니까 복사를 해주고, undirected graph니까 vertex v,w 는서로가 연결 되게 neighboring을 해준다.
Graph Traversal

다만, Graph의 경우 이렇게 Cycle이 있을 수 있으니 Visited 라는 것으로 방문했던 Node를 Check하는 기능을 추가 구현해야 한다.

Tree와 다르게 또 Disconnected Area가 있을 수 있기 때문에, 제일 outer에서 for loop을 돌려야 한다.
결국 Tree traversal과의 차이점 1. Cycle이 있으니 visited 활용 2. Disconnected graph를 위해 for loop을 돌려라
Tree 에선 child 지만, Graph에선 계층이 없으니 Neighbor이라고 표현한다.

처음으로 끝나는 8번의 함수! 노란색은 call 되었지만 끝나지 않은 놈. 흰 색은 call도 안 된 친구들이다.

이렇게 하면 Connected Area를 다 돌고, Disconnected area까지 점령이 가능하다.
DFT는 어디에 쓰나?
1. 특정 two vertices Connected? : for 문 안돌리고 한 vertex를 찍고 DFT 돌리면 둘이 연결되어 있는지 체크 가능
2. Graph가 Connected 이니? : 한 Node 찍고 돌린 다음에 DFT 돌리고 for문 돌릴 때 Visisted 아닌 놈 발견하면 Disconnected
3. Disjoint island 몇 개? : for문 돌리다가 DFTHelp에 들어가면 섬의 개수를 Counting 할 수 있다.
4. Cycle이 있니? : DFT 돌리다가 '나'를 다시 발견하게 되면 cycle이 있다.
요런 특징들을 이용해 코딩테스트 문제를 만들 수 있다.
복잡다.. 코드짜는 실전 연습좀 하고 와야겠다.
class BST:
def __init__(self) -> None :
self.root = None
def searchHelp(self,curNode:TreeNode,x:int) -> TreeNode:
if not curNode: return None
if x > curNode.val :
return self.searchHelp(curNode.right,x)
elif x < curNode.val :
return self.searchHelp(curNode.left,x)
else : return curNode
def search(self, x:int) -> TreeNode:
return self.searchHelp(self.root,x)
def insertHelp(self,curNode:TreeNode,x:int) -> TreeNode:
if not curNode : return TreeNode(x)
if x > curNode.val :
curNode.right = self.insertHelp(curNode.right,x)
elif x <= curNode.val :
curNode.left = self.insertHelp(curNode.left,x)
return curNode
def insert(self, x:int) -> None:
self.root = self.insertHelp(self.root,x)
def deleteHelp(self,curNode:TreeNode,x:int) -> TreeNode:
if not curNode : return None
# find
if x < curNode.val :
curNode.left = self.deleteHelp(curNode.left,x)
elif x > curNode.val :
curNode.right = self.deleteHelp(curNode.right,x)
else : # Find the target
# case 1 : 0 or 1 child
if not curNode.left :
return curNode.right
if not curNode.right :
return curNode.left
# case 2 : 2 children
temp = self.findmin(curNode.right)
curNode.val = temp.val
curNode.right = self.deleteHelp(curNode.right,temp.val)
# temp = self.deleteHelp(temp,temp.val) #temp란 놈이 None이 된다고 curNode.right이 사라지는 게 아니다.
print(temp)
return curNode
def delete(self, x:int) -> None:
self.root = self.deleteHelp(self.root,x)
def findmin(self, curNode:TreeNode) -> TreeNode:
while curNode.left :
curNode = curNode.left
return curNode # 오른쪽 subtree에서 제일 작은 것
def visit(self,curNode:TreeNode) -> None :
print(curNode.val)
# def BFT(self) -> None :
# if self.root == None : return
# q = [self.root]
# while q:
# curNode = q.pop(0)
# self.visit(curNode)
# if curNode.left:
# q.append(curNode.left)
# if curNode.right:
# q.append(curNode.right) #이렇게 해도 된다
def BFT(self) -> None:
if self.root == None : return
from collections import deque
q = deque([self.root])
while q:
curNode = q.popleft()
self.visit(curNode)
if curNode.left:
q.append(curNode.left)
if curNode.right:
q.append(curNode.right)
def DFT_pre(self) -> None:
self.DFT_preHelp(self.root)
def DFT_preHelp(self,curNode:TreeNode) -> None :
if not curNode : return
self.visit(curNode)
self.DFT_preHelp(curNode.left)
self.DFT_preHelp(curNode.right)
def DFT_in(self) -> None:
self.DFT_inHelp(self.root)
def DFT_inHelp(self,curNode:TreeNode) -> None :
if not curNode : return
self.DFT_inHelp(curNode.left)
self.visit(curNode)
self.DFT_inHelp(curNode.right)
def DFT_post(self) -> None:
self.DFT_postHelp(self.root)
def DFT_postHelp(self,curNode:TreeNode) -> None :
if not curNode : return
self.DFT_postHelp(curNode.left)
self.DFT_postHelp(curNode.right)
self.visit(curNode)
## test case
L = BST()
L.insert(15)
L.insert(10)
L.insert(20)
L.insert(8)
L.insert(12)
L.insert(17)
L.insert(25)
L.insert(18)
print("BFT:")
L.BFT()
print("DFT_pre:")
L.DFT_pre()
print("DFT_in:")
L.DFT_in()
print("DFT_post:")
L.DFT_post()
##
BFT:
15
10
20
8
12
17
25
18
DFT_pre:
15
10
8
12
20
17
18
25
DFT_in:
8
10
12
15
17
18
20
25
DFT_post:
8
12
10
18
17
25
20
15
- E. O. D -

'SW 만학도 > Python' 카테고리의 다른 글
| Review 11 - Data Indexed Array, Hash in Python (0) | 2024.07.10 |
|---|---|
| Review 9 - Queues & Stacks (0) | 2024.07.08 |
| Review 8 - Python Data Structure (1) | 2024.07.08 |
| Review 7 - Python Algorithm design & Testing & Debugging (0) | 2024.07.07 |
| Review 6 - Python Recursion & Merge Sort (0) | 2024.07.07 |