Review 6 - Python Search(Linear / Binary) & Sort(Selection / Insertion)
https://eglife.tistory.com/72 Review 5 - Python OOP(Objected Oriented Programming)https://eglife.tistory.com/68 Review 4 - Python File I/Ohttps://eglife.tistory.com/67 Review 3 - Loop & Set,Tuple,Dictionaries,Mutabilityhttps://eglife.tistory.com/66 Rev
eglife.tistory.com

Python에서 머리 깨지게 하는 녀석 중 하나인 Recursion!
Review를 해보자.
for / while loop은 어떤 i, j 같은 parameter가 loop를 진행하는데, 이건 Recursion이랑은 좀 다르다.
대표적인 Recursion 예시인 factorial로 코드를 알아봐보자
1. Recursion
# Factorial for 문
def facto(n:int) -> int :
ans = 1
for i in range(1,n+1):
ans *= i
return ans
# Factorial Recursion
def facto3(n:int) -> int:
if n==0 :
return 1
else :
return n*facto3(n-1)
전체 문제가 계속 비슷한 컨셉을 반복하면 Recursion을 쓸 수 있다.
즉, Subproblem의 구조(Structure)가 반복된다? Recurse 쓸 수 있다.
(근데 그 구조를 바라보는 안목 키우는 것이 쉽지가 않다 ; ;)
이 Recursion + Memory를 잘 쓰는 것을 Dynamic Programming 이라고 한다.
예를 들어, 5! 을 계산해야하는데 우리가 4! 의 값을 이미 메모리에 저장해놔서 이걸 사용하는 Case이다.
나중에 C++ 알고리즘 문제를 풀 때 설명할 것임 ㅠ

이런 구조는 수학적으로 연역적 X 귀납적 O 증명에서 사용된 방법이다.
EX : 모든 자연수에 대해 A 인 것이 참임을 증명하라 :
-> n = 1일때 가능한 거 보여주고, 자연수 n-1이 참일 때 자연수 n 이 A를 만족함을 보여주면 끝 ( Recursion )
# 피보나치 수열 예제
def fibonacci(n : int) -> int :
if n == 1 : return 1
elif n == 2 : return 2
return fibonacci(n-1) + fibonacci(n-2)
print(fibonacci(5))
print(fibonacci(1))
print(fibonacci(2))
print(fibonacci(10))
8
1
2
89
2. Merge Sort
지금껏 Insertion / Selection Sort를 했을 때 time은 O(N^2)이었다. 소요시간을 더 줄여보기 위해 뭔가 Sort를 Binary스럽게, log스럽게 해보는 시도를 한 것이 Merge Sort!

Recursion의 냄새가 난다. Step 2 에서 Recursion을 쓰면 된다.
Basecase는 list의 element가 1개인 경우라, Base 될 때까지 계속 쪼갠다
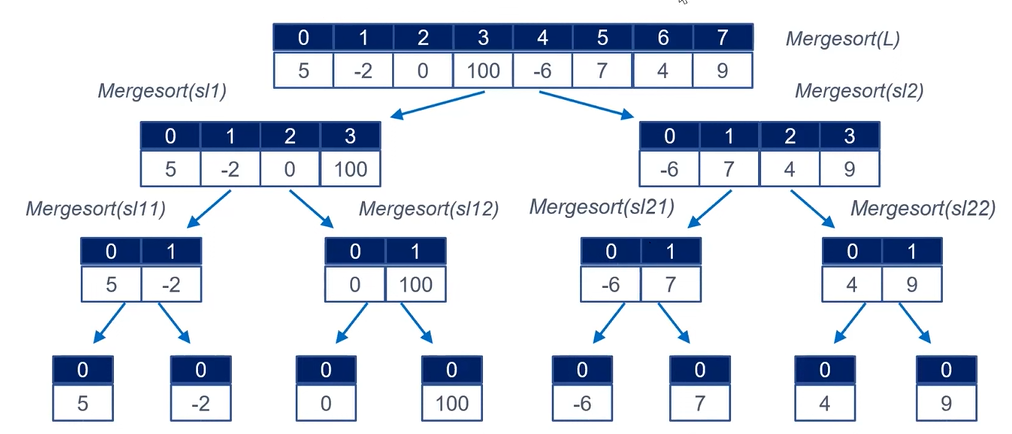
쪼개 놨던 걸 다시 Sorting 하는 과정이 Step 3 인데, 이건 두 list에서 제일 왼쪽 값끼리 비교해 작은거부터 채워나가면 자동으로 Sorting이 된 것이다.
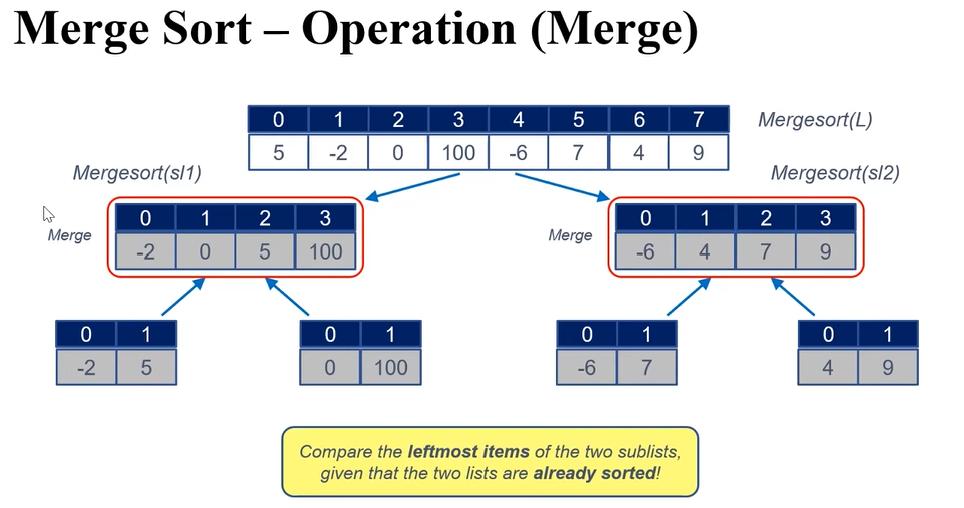
사실 이게 말이 쉽지, 실제로 코드 구현하는 건 좀 생소할 것이다..
3. Merge Sort Implementation
Merge Sort는 Insertion / Selection Sort와 달리 Memory를 더 써서 속도를 향상시키는 trade off를 이용한다.
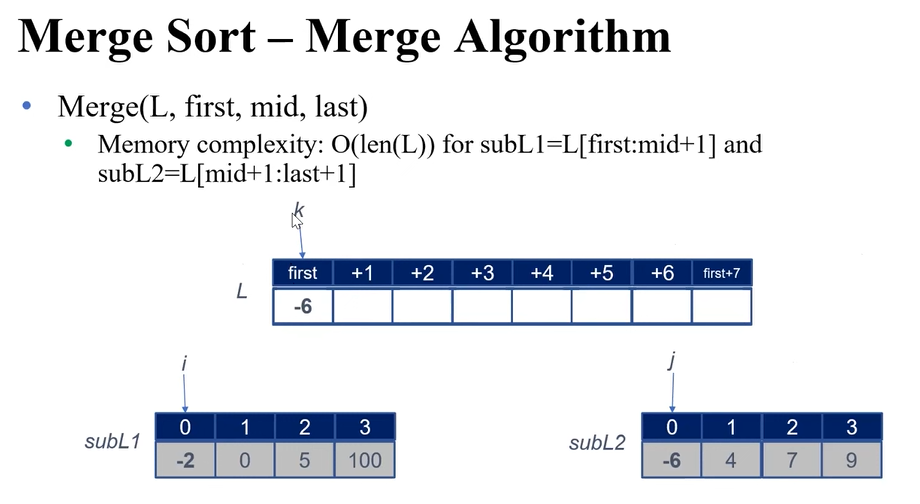
이 경우, Time Complexity는 O(len(L))이다. ( len(L)^2)이 아님! subL 들이 다 sorting이 되어있기 때문에, for문을 len(L)만큼 단 1회만 돌려도 Merge가 되는 시스템이다.

merge_sort, merge_sort_help, merge 함수를 각각 선언해줬다.
Merge Sort의 Time Complexity는 어떻게 되는가?
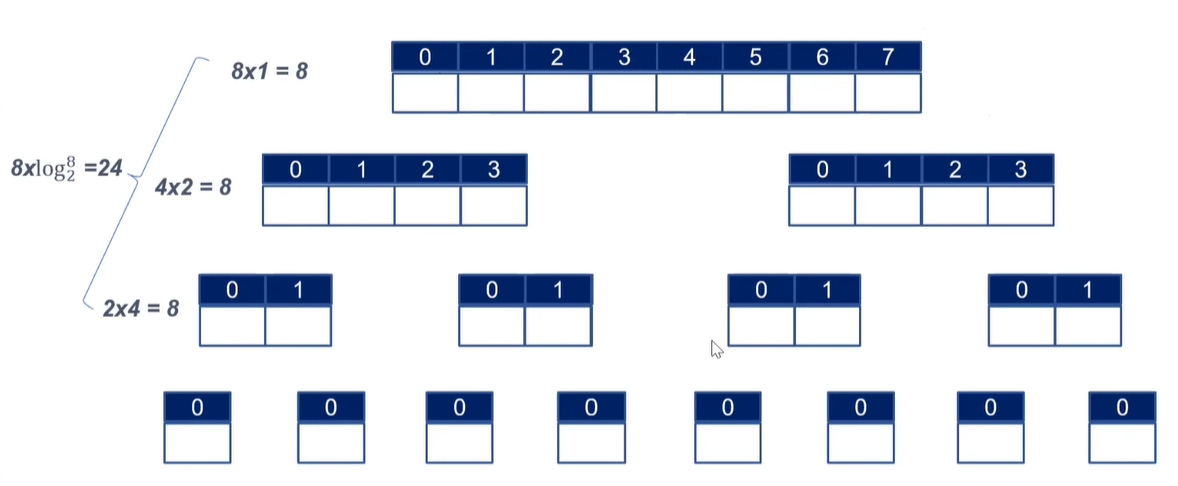
Merge 하는게 각 층마다 N만큼 Time이 발생한다. 그리고 층의 개수는 log N 이라서 결국 Time Complexity는 NlogN 으로 이득이다!
다만 기존에 없던 Memory 복사가 O(N)만큼 필요하다.

Python 내부 list.sort는 구현이 C로 되어있어서 속도가 더 빠르긴하지만, Merge Sort는 다른 Sort에 비해 완전히 빠른 알고리즘이다. log N 의 위력이 이렇게 크다는 것
Element 개수가 적을 땐 Merge 보다 Insertion Sort가 좀 더 빨라서 최근엔 merge + insert Sort인 #Tim sort가 있다. merge sort를 진행하다가 element가 32개 이하일 땐, Insertion sort로 전환하는 것이다.

- E. O . D -

'SW 만학도 > Python' 카테고리의 다른 글
| Review 8 - Python Data Structure (1) | 2024.07.08 |
|---|---|
| Review 7 - Python Algorithm design & Testing & Debugging (0) | 2024.07.07 |
| Review 6 - Python Search(Linear / Binary) & Sort(Selection / Insertion) (1) | 2024.07.05 |
| Review 5 - Python OOP(Objected Oriented Programming) (0) | 2024.07.05 |
| Review 4 - Python File I/O (1) | 2024.07.02 |