Algorithm Part의 기본적인 Data Structure인 Heap에 대해서 Implementation 연습을 시작해본다.
Heap의 경우 Priority Queue라고도 생각하면 되고, Max/Min Heap으로 구분된다.
특징으론 Max Heap을 예로 들었을 때, Heap Data 구조에 입력되는 Data는 크기가 큰 순서(Max)대로 우선순위를 갖은 체 저장된다.
이 말은, Heap에서 특정 Data를 꺼낼 때(Deque) 가장 크기가 큰 녀석이 추출되는 것이다.
일반적으로 우리가 아는 queue구조에서 우선 순위만 선입선출이 아닌, Data 크기에 따라 결정된다는 것을 알고 있으면 된다.
따라서, 내부에 저장된 Data를 임의로 Search 할 수는 없지만 우리가 정한 Logic( Max / Min 기준)으로 일종의 Queue처럼 Data를 넣고 빼고 관리할 수가 있다.
이 자료구조가 나중에 나오는 각종 Graph, Tree의 Shortest Path를 구하는 알고리즘에 기본적으로 쓰인다.
Heap 구조 자체를 정의해볼건데, Array로 만들거나 Tree 구조로 만들 수 있다.
이 두 가지에 대해서 Python / C / C++ 모두로 Heap 자료구조를 Implement 해볼 것이다.

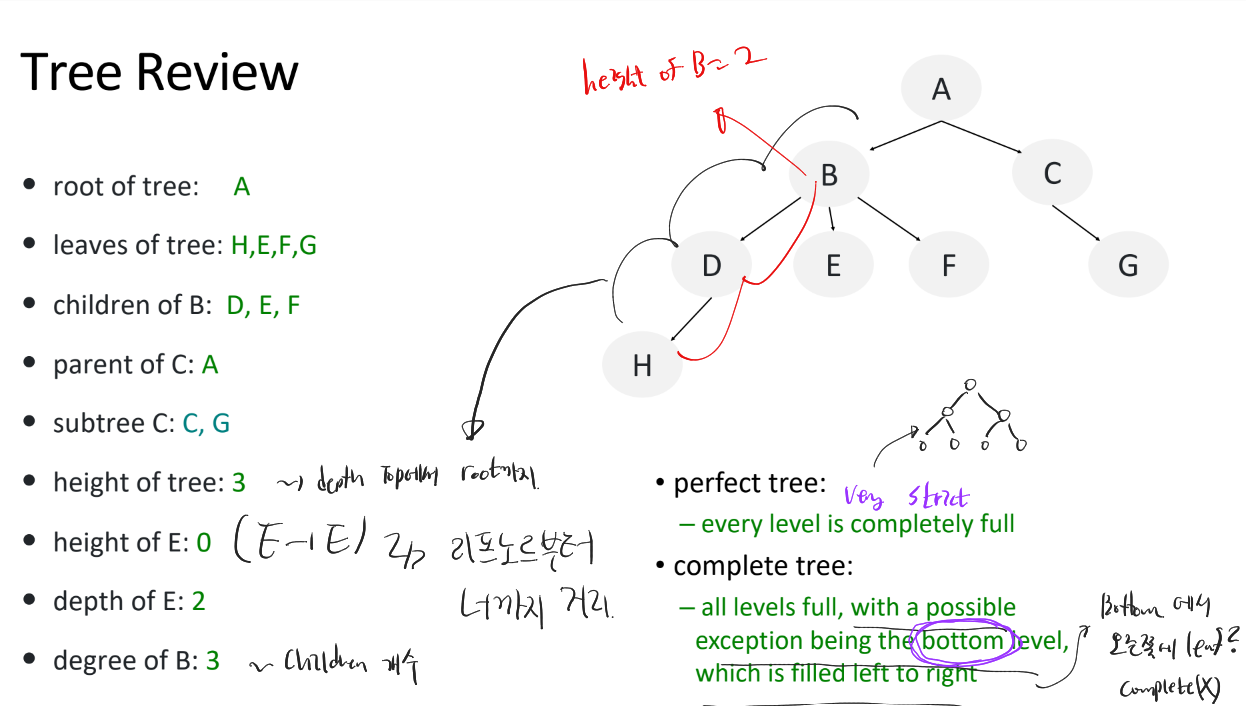
Heap은 BST가 아니라 Completed binary tree이다. parent과 children node 간의 대소비교만 유의미하고, Structure은 Left부터 차곡 차곡 쌓여있는 구조여야 한다.
Tree 구조의 기본적인 특성은 아래와 같다.
MAX-HEAP 기준으로 구현해보기
1. Python - Array
class MaxHeapArray:
def __init__(self, capacity):
"""
Initialize the MaxHeapArray with a fixed capacity.
Attributes:
- heap: List to store heap elements.
- capacity: Maximum number of elements in the heap.
- size: Current number of elements in the heap.
"""
self.heap = [0] * capacity # Array for the heap
self.capacity = capacity # Maximum capacity
self.size = 0 # Current number of elements in the heap
def parent(self, i):
"""Return the index of the parent node."""
return (i - 1) // 2
def left(self, i):
"""Return the index of the left child node."""
return 2 * i + 1
def right(self, i):
"""Return the index of the right child node."""
return 2 * i + 2
def insert_key(self, k):
"""Insert a new key into the heap."""
# Implementation here
if self.is_full():
print("Heap overflow: cannot insert key")
return
self.heap[self.size] = k
self.heapify_up(self.size)
self.size += 1
def extract_max(self):
"""Extract and return the maximum value from the heap."""
if self.is_empty() :
print("EMPTY")
return -1
else:
ans = self.heap[0]
self.heap[0],self.heap[self.size-1] = self.heap[self.size-1],self.heap[0]
self.size -= 1
self.heap[self.size] = None # Clear the last element (optional)
self.heapify_down(0)
return ans
def peek(self):
"""Return the maximum value without removing it."""
if self.is_empty() :
print("EMPTY")
return -1
else : return self.heap[0]
def heapify_up(self, i):
"""Restore the heap property from a node upwards."""
# Implementation here
##For Enqueue
while self.parent(i) >= 0 :# while i > 0 and self.heap[i] > self.heap[self.parent(i)]:
if self.heap[i] > self.heap[self.parent(i)]:
self.heap[self.parent(i)],self.heap[i]=self.heap[i],self.heap[self.parent(i)]
i = self.parent(i)
def heapify_down(self, i):
"""Restore the heap property from a node downwards."""
# Implementation here
##For Dequeue
while self.left(i) <= self.size-1 :
left = self.left(i)
right = self.right(i)
largest = i
if self.heap[largest] < self.heap[left]:
largest = left
if right <= self.size-1 and self.heap[largest] < self.heap[right] :
largest = right
if largest != i:
self.heap[largest],self.heap[i] = self.heap[i],self.heap[largest]
i = largest
else : break
def is_full(self):
"""Check if the heap is full."""
return self.size == self.capacity
def is_empty(self):
"""Check if the heap is empty."""
return self.size == 0
# Test cases for MaxHeapArray
print("Testing MaxHeapArray...\n")
max_heap = MaxHeapArray(10)
# Insertions
print("Inserting 10...")
max_heap.insert_key(10)
print("Heap:", max_heap.heap[:max_heap.size]) # Expected: [10]
print("Inserting 20...")
max_heap.insert_key(20)
print("Heap:", max_heap.heap[:max_heap.size]) # Expected: [20, 10]
print("Inserting 5...")
max_heap.insert_key(5)
print("Heap:", max_heap.heap[:max_heap.size]) # Expected: [20, 10, 5]
print("Inserting 15...")
max_heap.insert_key(15)
print("Heap:", max_heap.heap[:max_heap.size]) # Expected: [20, 15, 5, 10]
print("Inserting 25...")
max_heap.insert_key(25)
print("Heap:", max_heap.heap[:max_heap.size]) # Expected: [25, 20, 5, 10, 15]
# Peek
print("\nPeek maximum value:", max_heap.peek()) # Expected: 25
# Extract max
print("\nExtracting maximum value...")
print("Extracted:", max_heap.extract_max()) # Expected: 25
print("Heap after extraction:", max_heap.heap[:max_heap.size]) # Expected: [20, 15, 5, 10]
print("\nExtracting maximum value...")
print("Extracted:", max_heap.extract_max()) # Expected: 20
print("Heap after extraction:", max_heap.heap[:max_heap.size]) # Expected: [15, 10, 5]
# Check heap state
print("\nHeap size:", max_heap.size) # Expected: 3
print("Is heap empty?:", max_heap.is_empty()) # Expected: False
# Clear heap
print("\nClearing the heap...")
while not max_heap.is_empty():
print("Extracted:", max_heap.extract_max())
print("Is heap empty?:", max_heap.is_empty()) # Expected: True
1-2. Python - Tree
이번엔 Min-Heap을 Complete Binary Tree 구조로 구현해보기
class TreeNode:
def __init__(self, value):
"""Initialize a TreeNode."""
self.value = value
self.left = None
self.right = None
self.parent = None # Track the parent node for easier operations
class MinHeapTree:
def __init__(self):
"""Initialize an empty MinHeapTree."""
self.root = None
self.size = 0 # Number of nodes in the heap
def insert(self, value):
"""Insert a value into the Min Heap."""
new_node = TreeNode(value)
if not self.root:
self.root = new_node
else:
from collections import deque
q = deque()
q.append(self.root)
while q :
curr = q.popleft()
if not curr.left:
curr.left = new_node
new_node.parent = curr
break
else : q.append(curr.left)
if not curr.right:
curr.right = new_node
new_node.parent = curr
break
else : q.append(curr.right)
self._heapify_up(new_node)
self.size += 1
def extract_min(self):
"""Extract and return the minimum value (root) from the heap."""
# Implementation here
if self.size == 0 : return -1
ans = self.root.value
if self.size == 1 :
self.root = None
else:
from collections import deque
q = deque()
q.append(self.root)
temp = None
while q :
temp = q.popleft()
if temp.left :
q.append(temp.left)
if temp.right:
q.append(temp.right)
# temp 가 last node다
self.root.value = temp.value
if temp.parent:
if temp == temp.parent.left:
temp.parent.left = None
else : temp.parent.right = None
self._heapify_down(self.root)
self.size -= 1
return ans
def peek(self):
"""Return the minimum value (root) without removing it."""
# Implementation here
if self.size == 0 : return -1
else : return self.root.value
def _heapify_up(self, node):
"""Restore the Min Heap property from a node upwards."""
# Implementation here
while node.parent :
if node.parent.value > node.value :
# 부모 Node와 내 Node 바꾸는 게 쉽지 않네
# value만 바꿀까?
temp = node.value
node.value = node.parent.value
node.parent.value = temp
else : break
node = node.parent
def _heapify_down(self, node):
"""Restore the Min Heap property from a node downwards."""
if not node.left : return
smallest = node
if node.left and node.left.value < smallest.value:
smallest = node.left
if node.right and node.right.value < smallest.value:
smallest = node.right
if smallest != node:
node.value, smallest.value = smallest.value, node.value
self._heapify_down(smallest)
else : return
# Test cases for MinHeapTree
print("Testing MinHeapTree...\n")
min_heap = MinHeapTree()
# Insertions
print("Inserting 15...")
min_heap.insert(15)
print("Heap root:", min_heap.peek()) # Expected: 15
print("Inserting 10...")
min_heap.insert(10)
print("Heap root:", min_heap.peek()) # Expected: 10
print("Inserting 20...")
min_heap.insert(20)
print("Heap root:", min_heap.peek()) # Expected: 10
print("Inserting 5...")
min_heap.insert(5)
print("Heap root:", min_heap.peek()) # Expected: 5
print("Inserting 25...")
min_heap.insert(25)
print("Heap root:", min_heap.peek()) # Expected: 5
# Extract Min
print("\nExtracting minimum value...")
print("Extracted:", min_heap.extract_min()) # Expected: 5
print("Heap root:", min_heap.peek()) # Expected: 10
print("\nExtracting minimum value...")
print("Extracted:", min_heap.extract_min()) # Expected: 10
print("Heap root:", min_heap.peek()) # Expected: 15
# Clearing the heap
print("\nClearing the heap...")
while min_heap.size > 0:
print("Extracted:", min_heap.extract_min())
print("Heap is empty.")
# 모범답안
# class TreeNode:
# def __init__(self, value):
# self.value = value
# self.left = None
# self.right = None
# self.parent = None
# class MinHeapTree:
# def __init__(self):
# self.root = None
# self.size = 0
# def insert(self, value):
# """Insert a value into the Min Heap."""
# new_node = TreeNode(value)
# if not self.root:
# # If the heap is empty, set the root
# self.root = new_node
# else:
# # Perform level-order traversal to find the insertion point
# queue = [self.root]
# while queue:
# current = queue.pop(0)
# if not current.left:
# current.left = new_node
# new_node.parent = current
# break
# elif not current.right:
# current.right = new_node
# new_node.parent = current
# break
# queue.append(current.left)
# queue.append(current.right)
# # Restore the Min Heap property
# self._heapify_up(new_node)
# self.size += 1
# def extract_min(self):
# """Extract and return the minimum value (root) from the heap."""
# if not self.root:
# raise IndexError("Heap is empty!")
# min_value = self.root.value
# if self.size == 1:
# # If only one element exists, reset the heap
# self.root = None
# else:
# # Perform level-order traversal to find the last node
# queue = [self.root]
# last_node = None
# while queue:
# last_node = queue.pop(0)
# if last_node.left:
# queue.append(last_node.left)
# if last_node.right:
# queue.append(last_node.right)
# # Replace the root value with the last node value
# self.root.value = last_node.value
# # Remove the last node
# if last_node.parent:
# if last_node.parent.left == last_node:
# last_node.parent.left = None
# else:
# last_node.parent.right = None
# # Restore the Min Heap property
# self._heapify_down(self.root)
# self.size -= 1
# return min_value
# def peek(self):
# """Return the minimum value (root) without removing it."""
# if not self.root:
# raise IndexError("Heap is empty!")
# return self.root.value
# def _heapify_up(self, node):
# """Restore the Min Heap property from a node upwards."""
# while node.parent and node.value < node.parent.value:
# node.value, node.parent.value = node.parent.value, node.value
# node = node.parent
# def _heapify_down(self, node):
# """Restore the Min Heap property from a node downwards."""
# while node:
# smallest = node
# if node.left and node.left.value < smallest.value:
# smallest = node.left
# if node.right and node.right.value < smallest.value:
# smallest = node.right
# if smallest != node:
# node.value, smallest.value = smallest.value, node.value
# node = smallest
# else:
# break
2. C - Array
Max-Heap을 C의 Array형태로 표현해보기
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
typedef struct {
int *array; // Array to store the heap elements
int size; // Current number of elements in the heap
int capacity; // Maximum capacity of the heap
} MaxHeap;
// Function prototypes
MaxHeap* createHeap(int capacity){
MaxHeap* Heap = (MaxHeap*)malloc(sizeof(MaxHeap));
// Heap 생성 후 초기화 후 반환
Heap->capacity = capacity;
Heap->size = 0;
Heap->array = (int*)malloc(capacity*sizeof(int));
return Heap;
}
void insertKey(MaxHeap* heap, int key){ // Heaify-up
if(heap->size >= heap->capacity){
printf("FULL\n");
return;
}
heap->array[heap->size] = key;
heapifyUp(heap,heap->size);
heap->size++;
}
void swap(int* a, int* b){
int temp = *a;
*a = *b;
*b = temp;
}
int extractMax(MaxHeap* heap){ // Heaify-down
if(heap->size==0) return -1;
int ans = heap->array[0];
// 첫 / 마지막 value swap 후 첫 index를 heapifyDown
swap(&heap->array[0],&heap->array[heap->size-1]);
heap->array[heap->size-1] = NULL;
heap->size--;
heapifyDown(heap,0);
return ans;
}
int getMax(MaxHeap* heap){ // Clear
if(heap->size==0) return -1;
return heap->array[0];
}
void heapifyUp(MaxHeap* heap, int index){
int parent = (index-1)/2;
while((index-1)/2 >= 0){
parent = (index-1)/2;
if(heap->array[parent] < heap->array[index]){
// Swap
int temp = heap->array[index];
heap->array[index] = heap->array[parent];
heap->array[parent] = temp;
index = parent;
}
else break;
}
}
void heapifyDown(MaxHeap* heap, int index){
int left = 2*index + 1;
int right = 2*index + 2;
// Base case
if(left >= heap->size) return;
int largest = index;
if(heap->array[largest] < heap->array[left]){
largest = left;
}
if(right < heap->size && heap->array[largest] < heap->array[right]){
largest = right;
}
if(largest!=index){
// 값을 바꾸고, right or left 중 큰 index에서 다시 heapifyDown
swap(&heap->array[largest],&heap->array[index]);
heapifyDown(heap,largest);
}
else return;
}
void printHeap(MaxHeap* heap){ // Clear
printf("[");
for(int i=0;i<heap->size;i++){
printf("%d ",heap->array[i]);
}
printf("]\n");
}
void freeHeap(MaxHeap* heap){ // Clear
free(heap->array);
free(heap);
}
// Test cases
void runTestCases() {
printf("Testing MaxHeap...\n");
MaxHeap* heap = createHeap(10);
// Insert keys
printf("Inserting 10...\n");
insertKey(heap, 10);
printHeap(heap); // Expected: [10]
printf("Inserting 20...\n");
insertKey(heap, 20);
printHeap(heap); // Expected: [20, 10]
printf("Inserting 5...\n");
insertKey(heap, 5);
printHeap(heap); // Expected: [20, 10, 5]
printf("Inserting 15...\n");
insertKey(heap, 15);
printHeap(heap); // Expected: [20, 15, 5, 10]
printf("Inserting 25...\n");
insertKey(heap, 25);
printHeap(heap); // Expected: [25, 20, 5, 10, 15]
// Peek max
printf("\nMax value: %d\n", getMax(heap)); // Expected: 25
// Extract max
printf("\nExtracting max...\n");
printf("Extracted: %d\n", extractMax(heap)); // Expected: 25
printHeap(heap); // Expected: [20, 15, 5, 10]
printf("\nExtracting max...\n");
printf("Extracted: %d\n", extractMax(heap)); // Expected: 20
printHeap(heap); // Expected: [15, 10, 5]
printf("\nExtracting max...\n");
printf("Extracted: %d\n", extractMax(heap)); // Expected: 15
printHeap(heap); // Expected: [10, 5]
// Free the heap
freeHeap(heap);
printf("\nAll tests passed!\n");
}
int main(){
runTestCases();
}
/*
Solution
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
// Define the MaxHeap structure
typedef struct {
int *array; // Array to store the heap elements
int size; // Current number of elements in the heap
int capacity; // Maximum capacity of the heap
} MaxHeap;
// Function to create a MaxHeap
MaxHeap* createHeap(int capacity) {
MaxHeap* heap = (MaxHeap*)malloc(sizeof(MaxHeap));
heap->array = (int*)malloc(capacity * sizeof(int));
heap->size = 0;
heap->capacity = capacity;
return heap;
}
// Function to insert a key into the MaxHeap
void insertKey(MaxHeap* heap, int key) {
if (heap->size == heap->capacity) {
printf("Heap overflow: cannot insert key\n");
return;
}
// Insert the new key at the end
heap->array[heap->size] = key;
heap->size++;
// Restore the heap property
heapifyUp(heap, heap->size - 1);
}
// Function to extract the maximum value (root) from the heap
int extractMax(MaxHeap* heap) {
if (heap->size == 0) {
printf("Heap underflow: no elements to extract\n");
return INT_MIN;
}
// Store the maximum value
int max = heap->array[0];
// Replace the root with the last element
heap->array[0] = heap->array[heap->size - 1];
heap->size--;
// Restore the heap property
heapifyDown(heap, 0);
return max;
}
// Function to return the maximum value (root) without removing it
int getMax(MaxHeap* heap) {
if (heap->size == 0) {
printf("Heap is empty\n");
return INT_MIN;
}
return heap->array[0];
}
// Function to restore the heap property upwards
void heapifyUp(MaxHeap* heap, int index) {
int parent = (index - 1) / 2;
while (index > 0 && heap->array[index] > heap->array[parent]) {
// Swap the current element with its parent
int temp = heap->array[index];
heap->array[index] = heap->array[parent];
heap->array[parent] = temp;
// Move up the tree
index = parent;
parent = (index - 1) / 2;
}
}
// Function to restore the heap property downwards
void heapifyDown(MaxHeap* heap, int index) {
int largest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
// Check if the left child is larger
if (left < heap->size && heap->array[left] > heap->array[largest]) {
largest = left;
}
// Check if the right child is larger
if (right < heap->size && heap->array[right] > heap->array[largest]) {
largest = right;
}
// If the largest is not the current node, swap and continue heapifying
if (largest != index) {
int temp = heap->array[index];
heap->array[index] = heap->array[largest];
heap->array[largest] = temp;
heapifyDown(heap, largest);
}
}
// Function to print the heap
void printHeap(MaxHeap* heap) {
printf("Heap: ");
for (int i = 0; i < heap->size; i++) {
printf("%d ", heap->array[i]);
}
printf("\n");
}
// Function to free the heap memory
void freeHeap(MaxHeap* heap) {
free(heap->array);
free(heap);
}
// Main function to run test cases
int main() {
runTestCases();
return 0;
}
// Test cases
void runTestCases() {
printf("Testing MaxHeap...\n");
MaxHeap* heap = createHeap(10);
// Insert keys
printf("Inserting 10...\n");
insertKey(heap, 10);
printHeap(heap); // Expected: [10]
printf("Inserting 20...\n");
insertKey(heap, 20);
printHeap(heap); // Expected: [20, 10]
printf("Inserting 5...\n");
insertKey(heap, 5);
printHeap(heap); // Expected: [20, 10, 5]
printf("Inserting 15...\n");
insertKey(heap, 15);
printHeap(heap); // Expected: [20, 15, 5, 10]
printf("Inserting 25...\n");
insertKey(heap, 25);
printHeap(heap); // Expected: [25, 20, 5, 10, 15]
// Peek max
printf("\nMax value: %d\n", getMax(heap)); // Expected: 25
// Extract max
printf("\nExtracting max...\n");
printf("Extracted: %d\n", extractMax(heap)); // Expected: 25
printHeap(heap); // Expected: [20, 15, 5, 10]
printf("\nExtracting max...\n");
printf("Extracted: %d\n", extractMax(heap)); // Expected: 20
printHeap(heap); // Expected: [15, 10, 5]
// Free the heap
freeHeap(heap);
printf("\nAll tests passed!\n");
}
*/
2-2 C - Tree
Max Heap을 C programming으로 Tree구조형태 표현하기
C에서 Queue 비스무리하게 Array를 쓰는 신박한 표현방식을 배웠다.
print / free .. 기타 등등에 Queue를 따로 Container 선언해주지 않고 어떻게 index로 queue표현을 하는지 확인이 가능하니 아래 코드 참고!!
이 Queue도 다 쓰고 나면 free 해주라하는데, 깜빡했다.. 구찮아 죽겠네
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
// Define the structure for a tree node
typedef struct TreeNode {
int value;
struct TreeNode* left;
struct TreeNode* right;
struct TreeNode* parent;
} TreeNode;
// Define the structure for the Max Heap
typedef struct MaxHeap {
TreeNode* root; // Pointer to the root node
int size; // Current size of the heap
} MaxHeap;
// Function prototypes
MaxHeap* createHeap(){
MaxHeap* heap = (MaxHeap*)malloc(sizeof(MaxHeap));
// heap 객체 생성 후 초기화
heap->root = NULL;
heap->size = 0;
return heap;
};
TreeNode* createNode(int value){
TreeNode* new_node = (TreeNode*)malloc(sizeof(TreeNode));
new_node->value = value;
new_node->left = NULL;
new_node->right = NULL;
new_node->parent = NULL;
return new_node;
}
void heapifyUp(TreeNode* node);
void heapifyDown(TreeNode* node);
void insertKey(MaxHeap* heap, int value){
// Insert를 할 last node를 찾아야 한다.
TreeNode* new_node = createNode(value);
if(!heap->root){// root가 없는 경우
heap->root = new_node;
}else{ // root가 이미 있는 경우
TreeNode* q[heap->size];
int front = 0, rear = 0;
q[rear++] = heap->root;
while(front < rear){
TreeNode* curr = q[front++];
if(!curr->left){
curr->left = new_node;
new_node->parent = curr;
break;
}
if(!curr->right){
curr->right = new_node;
new_node->parent = curr;
break;
}
q[rear++] = curr->left;
q[rear++] = curr->right;
}
heapifyUp(new_node);
}
heap->size ++;
}
int extractMax(MaxHeap* heap){
if(!heap->root) return -1;
int ans = heap->root->value;
// root랑 맨 끝자락 놈이랑 SWAP 후 맨 끝자락 없애고 root heapdown
TreeNode* q[heap->size];
int front = 0, rear = 0;
q[rear++] = heap->root;
TreeNode* temp = NULL;
while(front<rear){
TreeNode* curr = q[front++];
temp = curr;
if(curr->left) q[rear++] = curr->left;
if(curr->right) q[rear++] = curr->right;
}
// temp는 이 Heap의 마지막 Node
// root만 있던 case
if(!temp->parent) heap->root = NULL;
else{
heap->root->value = temp->value;
if(temp == temp->parent->left){
temp->parent->left = NULL;
}else temp->parent->right = NULL;
free(temp);
}
heapifyDown(heap->root);
heap->size--;
return ans;
}
int getMax(MaxHeap* heap){ // Clear
if(heap->size == 0) return -1;
return heap->root->value;
}
void heapifyUp(TreeNode* node){
TreeNode* temp = node;
while(temp->parent){
if(temp->parent->value < temp->value){
// SWAPING
int swap = temp->value;
temp->value = temp->parent->value;
temp->parent->value = swap;
// SWAP Complete
temp = temp->parent;
}
else break;
}
}
void heapifyDown(TreeNode* node){
// Base Case
if(!node || !node->left) return;
TreeNode* largest = node;
if(largest->value < node->left->value){
largest = node->left;
}
if(node->right && largest->value < node->right->value){
largest = node->right;
}
if(largest != node){
// Value 끼리 swap
int temp = node->value;
node->value = largest->value;
largest->value = temp;
heapifyDown(largest);
}
else return;
}
void freeHeap(MaxHeap* heap){
TreeNode* q[heap->size+1]; // 넉넉하게 할당
int front = 0, rear = 0;
q[rear] = heap->root;
rear++;
while(front<rear){
TreeNode* curr = q[front];
front++;
if(curr->left){
q[rear] = curr->left;
rear++;
}
if(curr->right){
q[rear] = curr->right;
rear++;
}
free(curr);
}
free(heap);
}
void printHeap(TreeNode* root){
if(!root) return;
TreeNode* q[1000]; // 넉넉하게 할당
int front = 0, rear = 0;
q[rear] = root;
rear++;
printf("[");
while(front<rear){
TreeNode* curr = q[front];
front++;
printf("%d ",curr->value);
if(curr->left){
q[rear] = curr->left;
rear++;
}
if(curr->right){
q[rear] = curr->right;
rear++;
}
}
printf("]\n");
}
// Test case runner
void runTestCases(){
printf("Testing MaxHeap with Tree Nodes...\n");
MaxHeap* heap = createHeap();
// Insert keys
printf("Inserting 10...\n");
insertKey(heap, 10);
printHeap(heap->root); // Expected: 10
printf("Inserting 20...\n");
insertKey(heap, 20);
printHeap(heap->root); // Expected: 20, 10
printf("Inserting 5...\n");
insertKey(heap, 5);
printHeap(heap->root); // Expected: 20, 10, 5
printf("Inserting 15...\n");
insertKey(heap, 15);
printHeap(heap->root); // Expected: 20, 15, 5, 10
printf("Inserting 25...\n");
insertKey(heap, 25);
printHeap(heap->root); // Expected: 25, 20, 5, 10, 15
// Peek max
printf("\nMax value: %d\n", getMax(heap)); // Expected: 25
// Extract max
printf("\nExtracting max...\n");
printf("Extracted: %d\n", extractMax(heap)); // Expected: 25
printHeap(heap->root); // Expected: 20, 15, 5, 10
printf("\nExtracting max...\n");
printf("Extracted: %d\n", extractMax(heap)); // Expected: 20
printHeap(heap->root); // Expected: 15, 10, 5
// Free the heap
freeHeap(heap);
printf("\nAll tests passed!\n");
}
int main(){
runTestCases();
return 0;
}
/*
updated solution
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
// Define the structure for a tree node
typedef struct TreeNode {
int value;
struct TreeNode* left;
struct TreeNode* right;
struct TreeNode* parent;
} TreeNode;
// Define the structure for the Max Heap
typedef struct MaxHeap {
TreeNode* root;
int size;
} MaxHeap;
// Function to create a new Max Heap
MaxHeap* createHeap() {
MaxHeap* heap = (MaxHeap*)malloc(sizeof(MaxHeap));
heap->root = NULL;
heap->size = 0;
return heap;
}
// Function to create a new node
TreeNode* createNode(int value) {
TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
node->value = value;
node->left = NULL;
node->right = NULL;
node->parent = NULL;
return node;
}
// Function to insert a key into the Max Heap
void insertKey(MaxHeap* heap, int value) {
TreeNode* newNode = createNode(value);
heap->size++;
// If the heap is empty, set the new node as the root
if (!heap->root) {
heap->root = newNode;
return;
}
// Find the insertion point using level-order traversal
TreeNode* queue[heap->size];
int front = 0, rear = 0;
queue[rear++] = heap->root;
while (front < rear) {
TreeNode* curr = queue[front++];
if (!curr->left) {
curr->left = newNode;
newNode->parent = curr;
break;
} else {
queue[rear++] = curr->left;
}
if (!curr->right) {
curr->right = newNode;
newNode->parent = curr;
break;
} else {
queue[rear++] = curr->right;
}
}
// Restore the Max Heap property
TreeNode* node = newNode;
while (node->parent && node->value > node->parent->value) {
int temp = node->value;
node->value = node->parent->value;
node->parent->value = temp;
node = node->parent;
}
}
// Helper function to find the last node
TreeNode* findLastNode(TreeNode* root, int size) {
// Perform a level-order traversal to find the last node
TreeNode* queue[size + 1];
int front = 0, rear = 0;
queue[rear++] = root;
TreeNode* last = NULL;
while (front < rear) {
last = queue[front++];
if (last->left) queue[rear++] = last->left;
if (last->right) queue[rear++] = last->right;
}
return last;
}
// Function to extract the maximum value (root) from the heap
int extractMax(MaxHeap* heap) {
if (!heap->root) {
printf("Heap underflow: no elements to extract\n");
return -1;
}
int maxValue = heap->root->value;
TreeNode* lastNode = findLastNode(heap->root, heap->size);
if (lastNode == heap->root) {
free(heap->root);
heap->root = NULL;
heap->size--;
return maxValue;
}
// Replace root value with last node value
heap->root->value = lastNode->value;
// Remove last node
if (lastNode->parent->left == lastNode) {
lastNode->parent->left = NULL;
} else {
lastNode->parent->right = NULL;
}
free(lastNode);
heap->size--;
// Restore the Max Heap property
TreeNode* node = heap->root;
while (node->left) {
TreeNode* largest = node;
if (node->left && node->left->value > largest->value) {
largest = node->left;
}
if (node->right && node->right->value > largest->value) {
largest = node->right;
}
if (largest != node) {
int temp = node->value;
node->value = largest->value;
largest->value = temp;
node = largest;
} else {
break;
}
}
return maxValue;
}
// Function to return the maximum value without removing it
int getMax(MaxHeap* heap) {
if (!heap->root) {
printf("Heap is empty\n");
return -1;
}
return heap->root->value;
}
// Function to print the heap (level-order)
void printHeap(TreeNode* root) {
if (!root) {
printf("Heap is empty\n");
return;
}
TreeNode* queue[100];
int front = 0, rear = 0;
queue[rear++] = root;
while (front < rear) {
TreeNode* node = queue[front++];
printf("%d ", node->value);
if (node->left) queue[rear++] = node->left;
if (node->right) queue[rear++] = node->right;
}
printf("\n");
}
// Function to free the heap memory
void freeHeap(MaxHeap* heap) {
if (!heap->root) {
free(heap);
return;
}
TreeNode* queue[heap->size];
int front = 0, rear = 0;
queue[rear++] = heap->root;
while (front < rear) {
TreeNode* node = queue[front++];
if (node->left) queue[rear++] = node->left;
if (node->right) queue[rear++] = node->right;
free(node);
}
free(heap);
}
// Main function for testing
int main() {
printf("Testing MaxHeap with Tree Nodes...\n");
MaxHeap* heap = createHeap();
// Insert keys
printf("Inserting 10...\n");
insertKey(heap, 10);
printHeap(heap->root); // Expected: 10
printf("Inserting 20...\n");
insertKey(heap, 20);
printHeap(heap->root); // Expected: 20, 10
printf("Inserting 5...\n");
insertKey(heap, 5);
printHeap(heap->root); // Expected: 20, 10, 5
printf("Inserting 15...\n");
insertKey(heap, 15);
printHeap(heap->root); // Expected: 20, 15, 5, 10
printf("Inserting 25...\n");
insertKey(heap, 25);
printHeap(heap->root); // Expected: 25, 20, 5, 10, 15
// Extract max
printf("\nExtracting max...\n");
printf("Extracted: %d\n", extractMax(heap)); // Expected: 25
printHeap(heap->root); // Expected: 20, 15, 5, 10
freeHeap(heap);
printf("\nAll tests passed!\n");
return 0;
}
*/
Last One!!
3. C++ Array
Minheap 만들어보기
#include <iostream>
#include <vector>
#include <stdexcept>
using namespace std;
class MinHeap {
private:
vector<int> heap;
int parent(int i) { return (i - 1) / 2; }
int left(int i) { return 2 * i + 1; }
int right(int i) { return 2 * i + 2; }
void heapifyUp(int index){
while(parent(index)>=0){
if(heap[index] < heap[parent(index)]){
swap(heap[index],heap[parent(index)]);
index = parent(index);
}
else break;
}
}
void heapifyDown(int index){
if(left(index) >= heap.size()) return;
int smallest = index;
if(heap[smallest] > heap[left(index)]){
smallest = left(index);
}
if(right(index)<heap.size() && heap[smallest]>heap[right(index)]){
smallest = right(index);
}
if(smallest != index){
swap(heap[smallest],heap[index]);
heapifyDown(smallest);
}
}
public:
MinHeap() {}
// Inserts a key into the heap
void insert(int key){
heap.push_back(key);
heapifyUp(heap.size()-1);
}
// Extracts and returns the minimum value
int extractMin(){
if(heap.empty()) return -1;
int ans = heap[0];
swap(heap[0],heap[heap.size()-1]);
heap.pop_back();
heapifyDown(0);
return ans;
}
// Returns the minimum value without removing it
int getMin() const{
if(heap.empty()) return -1;
else return heap[0];
}
// Prints the heap for debugging
void printHeap() const{
cout << "[";
for(auto const x : heap){
cout << x << " ";
}
cout << "]" << endl;
}
};
// Test cases
void runTestCases() {
MinHeap minHeap;
cout << "Inserting 10..." << endl;
minHeap.insert(10);
minHeap.printHeap(); // Expected: [10]
cout << "Inserting 20..." << endl;
minHeap.insert(20);
minHeap.printHeap(); // Expected: [10, 20]
cout << "Inserting 5..." << endl;
minHeap.insert(5);
minHeap.printHeap(); // Expected: [5, 20, 10]
cout << "Inserting 15..." << endl;
minHeap.insert(15);
minHeap.printHeap(); // Expected: [5, 15, 10, 20]
cout << "Inserting 25..." << endl;
minHeap.insert(25);
minHeap.printHeap(); // Expected: [5, 15, 10, 20, 25]
cout << "\nMinimum value: " << minHeap.getMin() << endl; // Expected: 5
cout << "\nExtracting min..." << endl;
cout << "Extracted: " << minHeap.extractMin() << endl; // Expected: 5
minHeap.printHeap(); // Expected: [10, 15, 25, 20]
cout << "\nExtracting min..." << endl;
cout << "Extracted: " << minHeap.extractMin() << endl; // Expected: 10
minHeap.printHeap(); // Expected: [15, 20, 25]
}
int main() {
runTestCases();
return 0;
}
/*
Solution
#include <iostream>
#include <vector>
#include <stdexcept>
using namespace std;
class MinHeap {
private:
vector<int> heap;
int parent(int i) { return (i - 1) / 2; }
int left(int i) { return 2 * i + 1; }
int right(int i) { return 2 * i + 2; }
// Restore the Min Heap property upwards
void heapifyUp(int index) {
while (index > 0 && heap[index] < heap[parent(index)]) {
swap(heap[index], heap[parent(index)]);
index = parent(index);
}
}
// Restore the Min Heap property downwards
void heapifyDown(int index) {
int smallest = index;
int leftChild = left(index);
int rightChild = right(index);
if (leftChild < heap.size() && heap[leftChild] < heap[smallest]) {
smallest = leftChild;
}
if (rightChild < heap.size() && heap[rightChild] < heap[smallest]) {
smallest = rightChild;
}
if (smallest != index) {
swap(heap[index], heap[smallest]);
heapifyDown(smallest);
}
}
public:
MinHeap() {}
// Inserts a key into the heap
void insert(int key) {
heap.push_back(key);
heapifyUp(heap.size() - 1);
}
// Extracts and returns the minimum value
int extractMin() {
if (heap.empty()) {
throw runtime_error("Heap underflow: no elements to extract");
}
int minValue = heap[0];
heap[0] = heap.back();
heap.pop_back();
heapifyDown(0);
return minValue;
}
// Returns the minimum value without removing it
int getMin() const {
if (heap.empty()) {
throw runtime_error("Heap is empty");
}
return heap[0];
}
// Prints the heap for debugging
void printHeap() const {
cout << "[";
for (size_t i = 0; i < heap.size(); ++i) {
cout << heap[i];
if (i < heap.size() - 1) cout << ", ";
}
cout << "]" << endl;
}
};
// Test cases
void runTestCases() {
MinHeap minHeap;
cout << "Inserting 10..." << endl;
minHeap.insert(10);
minHeap.printHeap(); // Expected: [10]
cout << "Inserting 20..." << endl;
minHeap.insert(20);
minHeap.printHeap(); // Expected: [10, 20]
cout << "Inserting 5..." << endl;
minHeap.insert(5);
minHeap.printHeap(); // Expected: [5, 20, 10]
cout << "Inserting 15..." << endl;
minHeap.insert(15);
minHeap.printHeap(); // Expected: [5, 15, 10, 20]
cout << "Inserting 25..." << endl;
minHeap.insert(25);
minHeap.printHeap(); // Expected: [5, 15, 10, 20, 25]
cout << "\nMinimum value: " << minHeap.getMin() << endl; // Expected: 5
cout << "\nExtracting min..." << endl;
cout << "Extracted: " << minHeap.extractMin() << endl; // Expected: 5
minHeap.printHeap(); // Expected: [10, 15, 25, 20]
cout << "\nExtracting min..." << endl;
cout << "Extracted: " << minHeap.extractMin() << endl; // Expected: 10
minHeap.printHeap(); // Expected: [15, 20, 25]
}
int main() {
runTestCases();
return 0;
}
*/
뭔가 항상 C++로 하면 코드가 깔끔하고 빠르다.
괜히 사람들이 C++을 애용하는 것이 아니다!
3. C++ Tree
Minheap 만들어보기
긴 여정이었다..!
#include <iostream>
#include <queue>
using namespace std;
// Tree Node Structure
struct TreeNode {
int value;
TreeNode* left;
TreeNode* right;
TreeNode* parent;
TreeNode(int val) : value(val), left(nullptr), right(nullptr), parent(nullptr) {}
};
// MinHeapTree Class
class MinHeapTree {
private:
TreeNode* root;
int size;
void heapifyUp(TreeNode* node){
while(node->parent){
if(node->value < node->parent->value){
swap(node->value,node->parent->value);
node = node->parent;
}
else break;
}
}
void heapifyDown(TreeNode* node){
if(!node || !node->left) return;
TreeNode* smallest = node;
if(smallest->value > node->left->value){
smallest = node->left;
}
if(node->right && smallest->value > node->right->value){
smallest = node->right;
}
if(smallest!=node){
swap(node->value,smallest->value);
heapifyDown(smallest);
}
}
public:
MinHeapTree() : root(nullptr), size(0) {}
void insert(int value){
TreeNode* new_node = new TreeNode(value);
size++;
if(!root){
root = new_node;
return;
}
// 들어갈 자리를 찾고, 거기에 넣고, heapUP
queue<TreeNode*> q;
q.push(root);
while(!q.empty()){
TreeNode* curr = q.front();
q.pop();
if(!curr->left){
curr->left = new_node;
new_node->parent = curr;
break;
}
if(!curr->right){
curr->right = new_node;
new_node->parent = curr;
break;
}
q.push(curr->left);
q.push(curr->right);
}
heapifyUp(new_node);
}
int extractMin(){
if(!root) return -1;
int ans = root->value;
queue<TreeNode*> q;
q.push(root);
TreeNode* temp = nullptr;
while(!q.empty()){
TreeNode* curr = q.front();
temp = curr;
q.pop();
if(curr->left) q.push(curr->left);
if(curr->right) q.push(curr->right);
}
// 막 node와 root node value 스왑
swap(root->value,temp->value);
// temp 삭제
if(temp==root){
delete root;
root = nullptr;
}
else{
if(temp == temp->parent->left){
temp->parent->left = nullptr;
}else{
temp->parent->right = nullptr;
}
temp = nullptr;
}
// delete temp;
heapifyDown(root);
size--;
return ans;
}
int getMin() const{
if(!root) return -1;
return root->value;
}
void printHeap() const{
if(!root) return;
queue<TreeNode*> q;
q.push(root);
cout << "[ ";
while(!q.empty()){
TreeNode* curr = q.front();
q.pop();
cout << curr->value << " ";
if(curr->left) q.push(curr->left);
if(curr->right) q.push(curr->right);
}
cout<< " ]" << endl;
}
void freeHeap(){
if(!root) return;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()){
TreeNode* curr = q.front();
q.pop();
if(curr->left) q.push(curr->left);
if(curr->right) q.push(curr->right);
delete curr;
}
root = nullptr;
size = 0;
}
};
// Test cases
void runTestCases() {
MinHeapTree heap;
// Test 1: Insert single element and extract
cout << "Test 1: Insert single element and extract" << endl;
heap.insert(10);
heap.printHeap(); // Expected: [10]
cout << "Extracting min: " << heap.extractMin() << endl; // Expected: 10
heap.printHeap(); // Expected: []
// Test 2: Extract from an empty heap
cout << "\nTest 2: Extract from an empty heap" << endl;
cout << "Extracting min: " << heap.extractMin() << endl; // Expected: -1
// Test 3: Insert multiple elements in ascending order
cout << "\nTest 3: Insert multiple elements in ascending order" << endl;
heap.insert(5);
heap.insert(10);
heap.insert(15);
heap.insert(20);
heap.printHeap(); // Expected: [5, 10, 15, 20]
cout << "Extracting min: " << heap.extractMin() << endl; // Expected: 5
heap.printHeap(); // Expected: [10, 20, 15]
// Test 4: Insert multiple elements in descending order
cout << "\nTest 4: Insert multiple elements in descending order" << endl;
heap.insert(25);
heap.insert(1);
heap.insert(8);
heap.insert(3);
heap.printHeap(); // Expected: [1, 10, 8, 20, 25, 15, 3]
// Test 5: Repeated extraction until heap is empty
cout << "\nTest 5: Repeated extraction until heap is empty" << endl;
while (heap.getMin() != -1) {
cout << "Extracting min: " << heap.extractMin() << endl;
heap.printHeap();
}
// Test 6: Inserting into an empty heap after extraction
cout << "\nTest 6: Inserting into an empty heap after extraction" << endl;
heap.insert(50);
heap.insert(30);
heap.insert(40);
heap.insert(35);
heap.insert(45);
heap.printHeap(); // Expected: [30, 35, 40, 50, 45]
// Test 7: Insert duplicate values
cout << "\nTest 7: Insert duplicate values" << endl;
heap.insert(35);
heap.insert(40);
heap.printHeap(); // Expected: Duplicates should maintain heap order
cout << "Extracting min: " << heap.extractMin() << endl; // Expected: 30
// Test 8: Extract min repeatedly with duplicate values
cout << "\nTest 8: Extract min repeatedly with duplicate values" << endl;
while (heap.getMin() != -1) {
cout << "Extracting min: " << heap.extractMin() << endl;
heap.printHeap();
}
// Test 9: Insert into heap with large values
cout << "\nTest 9: Insert into heap with large values" << endl;
heap.insert(100000);
heap.insert(99999);
heap.insert(100001);
heap.insert(50000);
heap.printHeap(); // Expected: Heap maintains order even with large numbers
// Test 10: Stress test with multiple inserts and extracts
cout << "\nTest 10: Stress test with multiple inserts and extracts" << endl;
for (int i = 1; i <= 20; i++) {
heap.insert(i);
}
heap.printHeap(); // Check heap order
while (heap.getMin() != -1) {
cout << "Extracting min: " << heap.extractMin() << endl;
heap.printHeap();
}
// Test 11: Extract from empty heap after stress test
cout << "\nTest 11: Extract from empty heap after stress test" << endl;
cout << "Extracting min: " << heap.extractMin() << endl; // Expected: -1
// Free the heap
heap.freeHeap();
cout << "\nAll tests completed!" << endl;
}
int main() {
runTestCases();
return 0;
}
/*
Solution
#include <iostream>
#include <queue>
using namespace std;
// Tree Node Structure
struct TreeNode {
int value;
TreeNode* left;
TreeNode* right;
TreeNode* parent;
TreeNode(int val) : value(val), left(nullptr), right(nullptr), parent(nullptr) {}
};
// MinHeapTree Class
class MinHeapTree {
private:
TreeNode* root;
int size;
// Helper to perform heapify upwards
void heapifyUp(TreeNode* node) {
while (node->parent && node->value < node->parent->value) {
swap(node->value, node->parent->value);
node = node->parent;
}
}
// Helper to perform heapify downwards
void heapifyDown(TreeNode* node) {
while (node) {
TreeNode* smallest = node;
if (node->left && node->left->value < smallest->value) {
smallest = node->left;
}
if (node->right && node->right->value < smallest->value) {
smallest = node->right;
}
if (smallest != node) {
swap(node->value, smallest->value);
node = smallest;
} else {
break;
}
}
}
// Helper to find the last node in level-order
TreeNode* findLastNode() {
queue<TreeNode*> q;
q.push(root);
TreeNode* last = nullptr;
while (!q.empty()) {
last = q.front();
q.pop();
if (last->left) q.push(last->left);
if (last->right) q.push(last->right);
}
return last;
}
public:
MinHeapTree() : root(nullptr), size(0) {}
// Insert a value into the heap
void insert(int value) {
TreeNode* newNode = new TreeNode(value);
size++;
if (!root) {
root = newNode;
return;
}
// Find the insertion point using level-order traversal
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
TreeNode* curr = q.front();
q.pop();
if (!curr->left) {
curr->left = newNode;
newNode->parent = curr;
break;
} else if (!curr->right) {
curr->right = newNode;
newNode->parent = curr;
break;
}
q.push(curr->left);
q.push(curr->right);
}
// Restore the Min Heap property
heapifyUp(newNode);
}
// Extract and return the minimum value
int extractMin() {
if (!root) {
cout << "Heap underflow: no elements to extract\n";
return -1;
}
int minValue = root->value;
// Find the last node
TreeNode* lastNode = findLastNode();
// Replace root value with last node value
if (lastNode == root) {
delete root;
root = nullptr;
} else {
root->value = lastNode->value;
if (lastNode->parent->left == lastNode) {
lastNode->parent->left = nullptr;
} else {
lastNode->parent->right = nullptr;
}
delete lastNode;
// Restore the Min Heap property
heapifyDown(root);
}
size--;
return minValue;
}
// Get the minimum value without removing it
int getMin() const {
if (!root) {
cout << "Heap is empty\n";
return -1;
}
return root->value;
}
// Print the heap in level-order
void printHeap() const {
if (!root) {
cout << "Heap is empty\n";
return;
}
queue<TreeNode*> q;
q.push(root);
cout << "[";
while (!q.empty()) {
TreeNode* node = q.front();
q.pop();
cout << node->value << " ";
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
}
cout << "]" << endl;
}
// Free all nodes in the heap
void freeHeap() {
if (!root) return;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
TreeNode* node = q.front();
q.pop();
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
delete node;
}
root = nullptr;
size = 0;
}
};
// Test case runner
void runTestCases() {
MinHeapTree heap;
// Insertions
cout << "Inserting 10..." << endl;
heap.insert(10);
heap.printHeap(); // Expected: [10]
cout << "Inserting 20..." << endl;
heap.insert(20);
heap.printHeap(); // Expected: [10, 20]
cout << "Inserting 5..." << endl;
heap.insert(5);
heap.printHeap(); // Expected: [5, 20, 10]
cout << "Inserting 15..." << endl;
heap.insert(15);
heap.printHeap(); // Expected: [5, 15, 10, 20]
cout << "Inserting 25..." << endl;
heap.insert(25);
heap.printHeap(); // Expected: [5, 15, 10, 20, 25]
// Minimum value
cout << "\nMinimum value: " << heap.getMin() << endl; // Expected: 5
// Extract min
cout << "\nExtracting min..." << endl;
cout << "Extracted: " << heap.extractMin() << endl; // Expected: 5
heap.printHeap(); // Expected: [10, 15, 25, 20]
// Free heap
heap.freeHeap();
}
*/'SW 만학도 > C++ & Algorithm' 카테고리의 다른 글
| Review 11 - Dynamic Programming (0) | 2024.08.03 |
|---|---|
| Review 10 - Single-Source-Shortest Path in C++ (0) | 2024.08.02 |
| Review 9 - MST(Minimum Spanning Trees) in C++ (8) | 2024.07.24 |
| [Algorithm] Review 8 - Priority Queues and Heaps in C++ (3) | 2024.07.22 |
| [Main course!] Review 7 - Inheritance in C++ (0) | 2024.07.21 |