https://leetcode.com/problems/min-cost-to-connect-all-points/description/
You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.
Example 1:
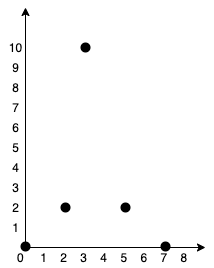
Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20
Explanation: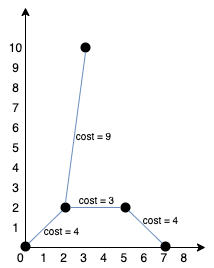
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
Example 2:
Input: points = [[3,12],[-2,5],[-4,1]]
Output: 18
Constraints:
- 1 <= points.length <= 1000
- -106 <= xi, yi <= 106
- All pairs (xi, yi) are distinct.
예전에 C++ 알고리즘 Minimum spanning tree 공부한다고 풀었던 기록이 있는데,
다시 보니까 그저 새롭다.
인간은 망각의 동물
다시 한 번 풀어보자
1. Python
아 진짜 간신히 풀어냈건만 또 time - limit에 걸렸다. 이중 for문이라 O(N^2)이긴 한데, 아오 좀 결과만 나오면 좀 넘어가주지 이것들이 ;;
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int:
# for single point, just connect with the closet one?
ans = 0
n = len(points)
visited = [points[0]]
def man(point1:list[int],point2:list[int]) -> int:
return abs(point1[0]-point2[0])+abs(point1[1]-point2[1])
while n != 1 :
temp = 10000000
min_val = [0,0]
for x in visited:
for point in points :
if point not in visited and temp > man(x,point):
temp = man(x,point)
min_val = point
ans += temp
visited.append(min_val)
n-=1
return ans
while문 안에 이중 for문이 화근이다.
잔인한 leetcode.. 무지막지한 test case에 GG선언이다 ㅠㅠ

그 이름도 유명한 Prims 또는 Kruskal Algorithm으로 풀어야 헌다.
- Prims
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int:
def man(point1,point2): return abs(point1[0]-point2[0])+abs(point1[1]-point2[1])
n = len(points)
ans = 0
min_heap = [[0,0]]
in_mst = [False] * n
edge_used = 0
while edge_used < n :
cost, u = heappop(min_heap)
if in_mst[u] :
continue
in_mst[u] = True
ans += cost
edge_used +=1
for v in range(n):
if not in_mst[v]:
heappush(min_heap,([man(points[u],points[v]),v]))
return ans
2. C++
class Solution {
public:
int minCostConnectPoints(vector<vector<int>>& points) {
int n = points.size();
if(n == 1) return 0;
int used = 0;
vector<int> visited(n,false);
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> mq;
mq.push({0,0});
int ans = 0;
while(used < n){
int cost = mq.top().first;
int v = mq.top().second;
mq.pop();
if(visited[v]) continue;
ans += cost;
visited[v] = true;
used++;
for(int i=0;i<n;i++){
if(!visited[i]){
mq.push({abs(points[i][0]-points[v][0])+abs(points[i][1]-points[v][1]),i});
}
}
}
return ans;
}
};
고생했다!!
잊지 말자 Prims, Kruskal은 Heap 이용이고,
Python엔 Min-heap만 있으며 C++에선 Max-heap이 default이고 min heap은 initialize 할 때 greater과 같이 스끼다시좀 섞어주면 된다.
밑은, 참고차 공유하는 Kruskal Algorithm
#include <stdio.h>
#include <stdlib.h>
#define MAX 100
#define INF 1000000
typedef struct {
int u, v, cost;
} Edge;
Edge edges[MAX];
int parent[MAX];
// Union-Find 함수
int find(int i) {
while (parent[i] != i)
i = parent[i];
return i;
}
void unionSets(int i, int j) {
int rootI = find(i);
int rootJ = find(j);
parent[rootI] = rootJ;
}
// 간선의 비용 기준으로 정렬하는 함수
int compareEdges(const void *a, const void *b) {
return ((Edge *)a)->cost - ((Edge *)b)->cost;
}
// 크루스칼 알고리즘
void kruskal(int numVertices, int numEdges) {
int mstCost = 0, edgesUsed = 0;
// 초기화
for (int i = 0; i < numVertices; i++)
parent[i] = i;
// 간선을 비용 기준으로 정렬
qsort(edges, numEdges, sizeof(Edge), compareEdges);
// 최소 스패닝 트리 구성
for (int i = 0; i < numEdges && edgesUsed < numVertices - 1; i++) {
int u = edges[i].u;
int v = edges[i].v;
int cost = edges[i].cost;
if (find(u) != find(v)) { // 사이클이 생기지 않으면 추가
unionSets(u, v);
printf("Edge (%d, %d) with cost %d added to MST\n", u, v, cost);
mstCost += cost;
edgesUsed++;
}
}
printf("Minimum cost to connect all vertices: %d\n", mstCost);
}
int main() {
int numVertices = 4;
int numEdges = 5;
edges[0] = (Edge){0, 1, 10};
edges[1] = (Edge){0, 2, 6};
edges[2] = (Edge){0, 3, 5};
edges[3] = (Edge){1, 3, 15};
edges[4] = (Edge){2, 3, 4};
kruskal(numVertices, numEdges);
return 0;
}'Coding_Practice' 카테고리의 다른 글
| Generate Parentheses[String,Dynamic Programming,Backtracking] (1) | 2024.11.14 |
|---|---|
| Maximal Square(Array,Dynamic Programming,Matrix) (0) | 2024.11.13 |
| Min Cost Climbing Stairs(Array,Dynamic Programming) (0) | 2024.11.11 |
| Valid Palindrome(Two Pointers,String) (2) | 2024.11.11 |
| Minimum One Bit Operations to Make Integers Zero[Dynamic Programming,Bit Manipulation,Memoization] (2) | 2024.11.08 |