Algortihm의 대표적인 친구들인 MST, SSSP, APSP에 대한 이론 공부 Review를 빠르게 진행해보려고 한다.
한 번씩 봤던 내용이니까 이론을 빨리 다루고, Code와 익숙해져보자.
각각의 경우 종류는 많지만, 대표적으로 쓰이는 몇 가지만 적어보려고 한다.
1. Minimum Spanning Tree
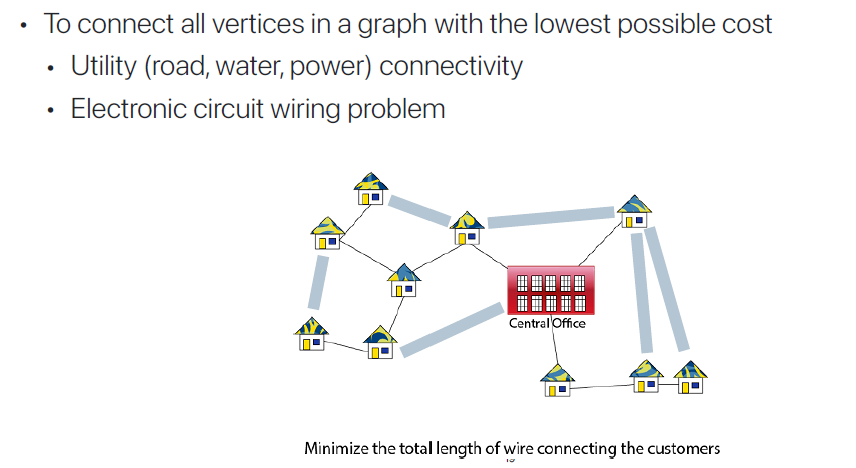
한 Grpah에서 가장 낮은 cost로 전체 vertices를 도는 것을 계산하는 알고리즘이다.
그리고 여기서 Spanning Tree란, 어떤 Graph의 모든 Vertex를 다 포함하고 있는연결구조를 말한다.
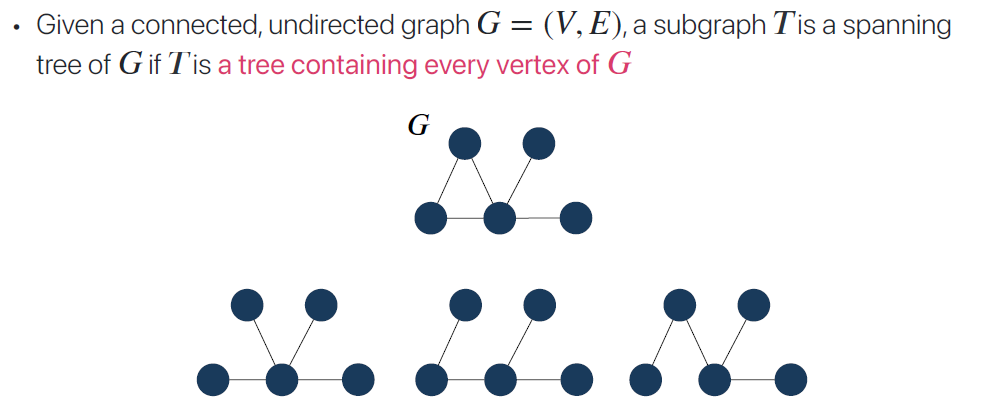
개중에 가장 Total Weight 이 작은 친구를 Minimum Spanning Tree라고 부르는 것이다.
이 MST 중 가장 유명한 알고리즘 2개를 다루겠다.
첫 번째, Prim's Algorithm
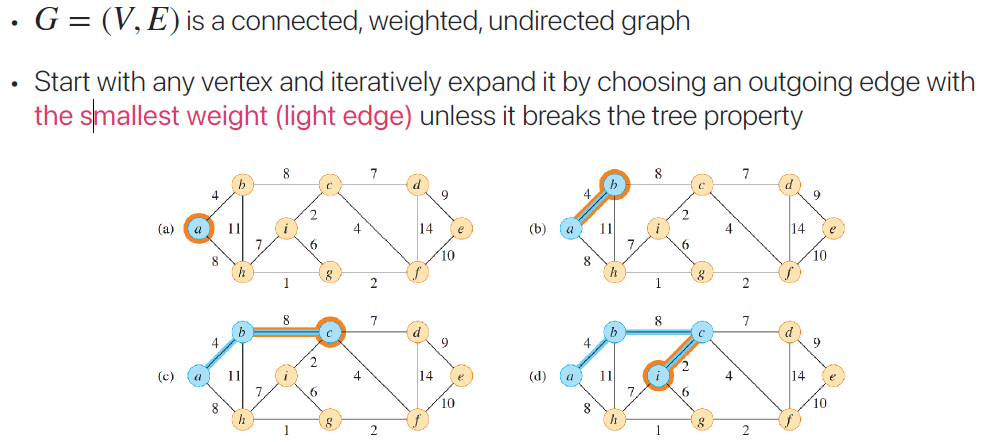
아무 Vertex에서 시작하여, Edge를 넓혀가는데 연결되어 Tree를 형성한 vertex들 기준으로 가장 작은 weight을 하나씩 연결해간다. 단, 이 때 tree의 property를 어기면 안 된다.(Cycle을 형성하면 안 됨, 즉 이미 visit 한 Vertex가 다시 추가되면 안 됨)

Prim's Algorithm의 Time complexity는 : O(E log V ) 이다.
두 번 째, Kruskal's Algorithm
Kruskal 알고리즘은, Graph에서 Minimum edge를 하나씩 추가해 Spanning 하는 것이다. 이 때도 역시, tree propery를 깨면 안 된다.
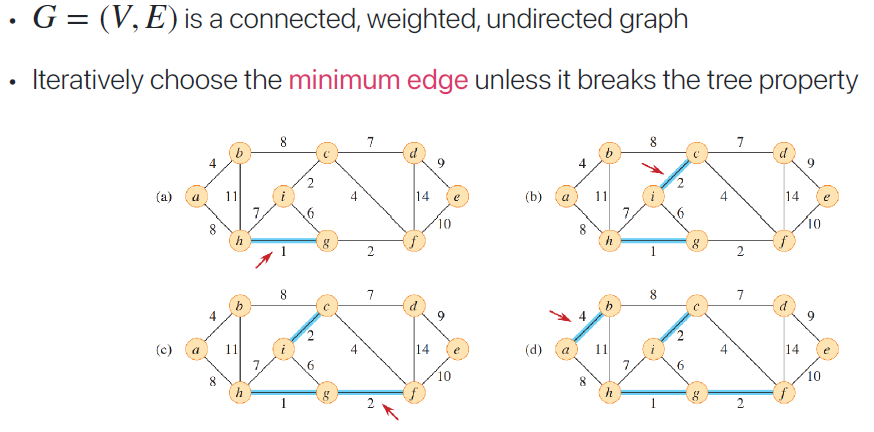
이 알고리즘엔, Union - Find 알고리즘이 쓰인다.

Kruskal Algorithm의 Time Complexity는 역시나 O( E log V ) 이다.
정리하자면, MST는 Connected / Undirected Graph에서 모든 Vetices를 방문하는 최소 Weight의 Tree 구조를 말한다. Prim's 는 한 single vertex에서 출발하여 Smallest vertex를 하나씩 연결해 나가는 것이고, Kruskal은 일단 edge를 weight순으로 오름차순 정렬한 다음에 cycle이 만들어지지 않는 선에서 작은 weight edge부터 하나씩 tree에 추가해 나가는 Algorithm이다.
MST의 코드 구현은 아래와 같다.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int prim(int n, vector<vector<pair<int, int>>> &graph) {
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
vector<bool> inMST(n, false);
pq.push({0, 0}); // cost & node
int mst_cost = 0;
while(!pq.empty()){
pair<int,int> temp = pq.top();
pq.pop();
int w = temp.first;
int u = temp.second;
if(inMST[u]) continue; // 기 방문 노드인지 확인
inMST[u] = true;
mst_cost += w;
for(const auto p : graph[u]){
if(!inMST[p.first]) pq.push({p.second,p.first});
}
}
return mst_cost;
}
int main(){
int n = 4;
vector<vector<pair<int, int>>> graph(n);
graph[0] = {{1, 1}, {2, 4}};
graph[1] = {{0, 1}, {2, 3}, {3, 5}};
graph[2] = {{0, 4}, {1, 3}, {3, 2}};
graph[3] = {{1, 5}, {2, 2}};
cout << "MST COST(Prims) : " << prim(n,graph) << endl; // 6
}
개인적으로 Kruskal 은 Union - Find 이던데,, 너무 어렵다.
GG!
// Kruskal -------------> GG 크루스칼 너무 어렵다..
#include <iostream>
#include <vector>
#include <tuple>
#include <algorithm>
using namespace std;
vector<int> parent, rank_set; // 🔹 'rank' 대신 'rank_set' 사용하여 충돌 방지
// 🔹 MAKE-SET(v): 모든 정점을 독립적인 집합으로 초기화
void make_set(int n) {
parent.resize(n);
rank_set.resize(n, 0);
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
// 🔹 FIND-SET(u): 정점 u의 대표(루트)를 찾음 (경로 압축 적용)
int find_set(int u) {
if (parent[u] != u)
parent[u] = find_set(parent[u]); // 경로 압축
return parent[u];
}
// 🔹 UNION(u, v): 두 집합을 합침 (랭크 기반)
void union_sets(int u, int v) {
u = find_set(u);
v = find_set(v);
if (u != v) {
if (rank_set[u] > rank_set[v]) swap(u, v); // 작은 랭크를 큰 랭크에 붙임
parent[u] = v;
if (rank_set[u] == rank_set[v]) rank_set[v]++;
}
}
// 🔹 크루스칼 알고리즘 (MST 구하기)
int kruskal(int n, vector<tuple<int, int, int>> &edges) {
make_set(n);
sort(edges.begin(), edges.end()); // 가중치 기준 정렬
int mst_cost = 0;
vector<pair<int, int>> mst_edges;
for (auto [w, u, v] : edges) {
if (find_set(u) != find_set(v)) { // 사이클이 생기지 않는 경우
union_sets(u, v);
mst_cost += w;
mst_edges.push_back({u, v});
}
}
// 🔹 MST 결과 출력
cout << "MST Edges:\n";
for (auto [u, v] : mst_edges) {
cout << u << " - " << v << endl;
}
return mst_cost;
}
// 🔹 메인 함수 (그래프 생성 및 크루스칼 실행)
int main() {
int n = 4; // 정점 개수
vector<tuple<int, int, int>> edges = { // 가중치, 노드 a, 노드 b
{1, 0, 1}, {3, 1, 2}, {4, 0, 2}, {2, 2, 3}, {5, 1, 3}
};
cout << "Minimum Spanning Tree Cost (Kruskal): " << kruskal(n, edges) << endl;
return 0;
}
걍 Kruskal은 Edge 추가 해나가는 방식, Prims는 근처 Node 하나씩 추가해나가는 방식으로 이해하고 있자.
2. SSSP
SSSP는 Weighted / Directed graph 에선 특정 vertex S를 기준으로 모든 vertex를 다 돌았을 때 total weight이 최소가 되는 Path이고 Vertex 간 길이 없어서 도달할 수 없는 경우 Weght는 INT_MAX이다.
그리고, 여러 SSSP가 중복으로 존재할 수 있다.
관련된 알고리즘으론,
첫 번 째 Dijkstra's Algorithm
Weighted, Directed Graph 의 알고리즘이고, Non - Negative edge weight을 가정한다.
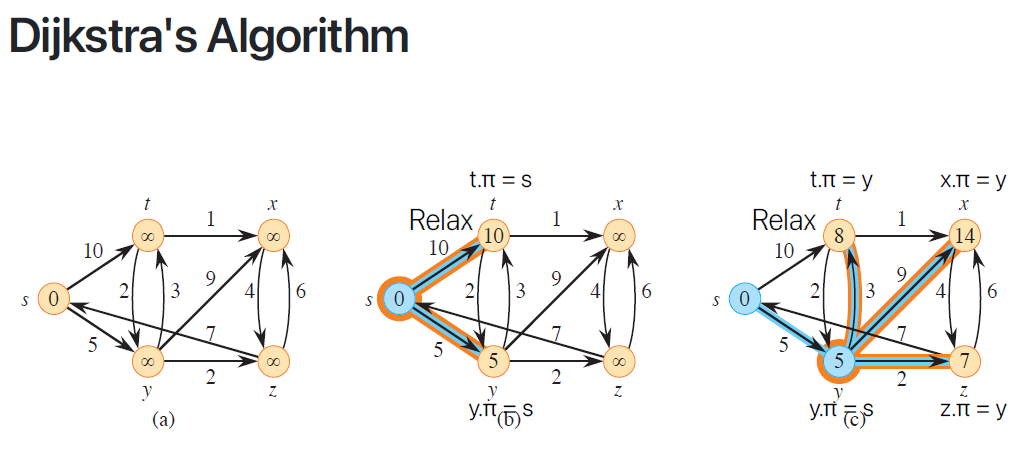

Time complexity 는 O( ( V + E ) log V ) 이다.
MST와 SSSP를 비교해보면, MST는 특정 vertex를 기준으로 한 Shortest Path를 제시하지 않는다.
그저 Graph 내의 모든 Vertex들이 다 연결만 되어 있으면 될 뿐...
두 번 째는 Bellman-Ford Algorithm
다익스트라에서, edge가 Negative 인 경우를 허용할 때 적용할 수 있는 알고리즘이다.
그러다보니, 중간에 Negative - Weight Cycle이 있는지 확인이 필요하다. (Shortest Path 계산시 무한한 음수로 발산할 수 있기에)

Bellman Ford 의 iteration은 MAX # Vertex - 1 회 돈다. 그래야 SSSP가 만들어지기 때문이다.
이 둘의 코드는 아래와 같다.
// #include <iostream>
// #include <vector>
// #include <queue>
// #include <limits>
// using namespace std;
// // 무한대 값 설정
// const int INF = numeric_limits<int>::max();
// // 그래프의 노드 표현 구조체
// struct Edge {
// int to;
// int weight;
// };
// // 다익스트라 알고리즘 실행 함수
// vector<int> dijkstra(int n, vector<vector<Edge>>& adj, int start) {
// vector<int> dist(n, INF); // 최단 거리 저장 배열
// vector<int> parent(n, -1); // 경로 추적 배열
// priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> minHeap;
// // 시작 노드 초기화
// dist[start] = 0;
// minHeap.push({0, start});
// while (!minHeap.empty()) {
// int d = minHeap.top().first;
// int u = minHeap.top().second;
// minHeap.pop();
// // 현재 거리가 기존 저장된 거리보다 크면 스킵
// if (d > dist[u]) continue;
// // 인접 노드 탐색
// for (const Edge& edge : adj[u]) {
// int v = edge.to;
// int weight = edge.weight;
// // Relaxation
// if (dist[v] > dist[u] + weight) {
// dist[v] = dist[u] + weight;
// parent[v] = u;
// minHeap.push({dist[v], v});
// }
// }
// }
// return dist; // 최단 거리 반환
// }
// // main 함수: 테스트 실행
// int main() {
// int n = 6; // 노드 개수
// vector<vector<Edge>> graph(n);
// // 그래프 추가 (양방향 그래프라면 양쪽에 추가)
// graph[0].push_back({1, 10});
// graph[0].push_back({2, 5});
// graph[1].push_back({2, 2});
// graph[1].push_back({3, 1});
// graph[2].push_back({1, 3});
// graph[2].push_back({3, 9});
// graph[2].push_back({4, 2});
// graph[3].push_back({4, 4});
// graph[4].push_back({5, 6});
// graph[3].push_back({5, 7});
// int start = 0; // 시작 노드 (예: 0번 노드에서 시작)
// vector<int> shortestDistances = dijkstra(n, graph, start);
// // 결과 출력
// cout << "start from -> " << start << endl;
// for (int i = 0; i < n; i++) {
// cout << "NODE " << i << ": ";
// if (shortestDistances[i] == INF)
// cout << "impossible" << endl;
// else
// cout << shortestDistances[i] << endl;
// }
// return 0;
// }
// Bellman Ford
#include <iostream>
#include <vector>
#include <limits>
using namespace std;
// Infinite distance (for initialization)
const int INF = numeric_limits<int>::max();
// Graph edge structure
struct Edge {
int from, to, weight;
};
// Bellman-Ford Algorithm
bool bellmanFord(int n, vector<Edge>& edges, int start, vector<int>& dist) {
dist.assign(n, INF); // Initialize distances
dist[start] = 0;
// Relax all edges (V-1) times
for (int i = 0; i < n - 1; i++) {
bool updated = false;
for (const Edge& edge : edges) {
if (dist[edge.from] != INF && dist[edge.to] > dist[edge.from] + edge.weight) {
dist[edge.to] = dist[edge.from] + edge.weight;
updated = true;
}
}
if (!updated) break; // Optimization: Stop if no updates
}
// Check for negative-weight cycles
for (const Edge& edge : edges) {
if (dist[edge.from] != INF && dist[edge.to] > dist[edge.from] + edge.weight) {
return false; // Negative cycle detected
}
}
return true;
}
// Main function for testing
int main() {
int n = 5; // Number of nodes
vector<Edge> edges = {
{0, 1, 6}, {0, 2, 7}, {1, 2, 8}, {1, 3, 5},
{1, 4, -4}, {2, 3, -3}, {2, 4, 9}, {3, 1, -2},
{4, 3, 7}, {3, 0, 2}
};
int start = 0;
vector<int> distances;
bool success = bellmanFord(n, edges, start, distances);
if (!success) {
cout << "Negative cycle detected. No shortest path possible." << endl;
} else {
cout << "Shortest distances from source " << start << ":" << endl;
for (int i = 0; i < n; i++) {
cout << "Node " << i << ": ";
if (distances[i] == INF)
cout << "Unreachable" << endl;
else
cout << distances[i] << endl;
}
}
return 0;
}
그리고 추가로 SSSP for Directed Acyclic Graphs (DAGs)

3. APSP
APSP는 특정 pair of verticle 사이에서 가장 짧은 Path를 찾는 기법이다.
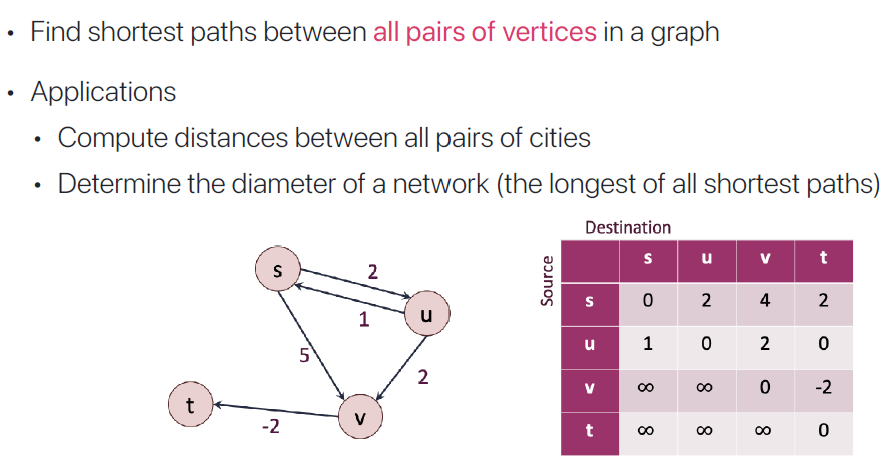
APSP는 Weighted Directed graph 에서 input으로 n 개의 verices, n * n adjacency matrix를 넣는다.
이 Adjacency Matrix의 조건은 아래와 같다.

역시나 Negative Weight Cycle은 없다고 가정한다.
Output으론 n * n shortest path weight이 적힌 Matrix L을 반환한다.
Dijkstra / Bellman Ford 알고리즘을 이용해서 풀어도 된다.

근데 이럴 경우 time complexity가 너~~무 높다..
그래서 착안한 2가지 방법
첫 번 째 Floyd - Warshall Algorithm
일단 기본적으로 weight - directed graph이면서 negative weight가 있는 건 허용이 되는데 cycle은 안 된다.
O(N^3)에 빛나는 플로이드 워셜 알고리즘..

for문 3개 돌려서 해결한다.
그리고 두 번 째 Johnson's Algorithm
보통 Sparse 한 graph에서 Dijkstra 알고리즘을 모든 Vertex에 대해서 실행하는 것이 가장 속도가 빠르다는 점에 착안한다. Dijkstra를 쓰는 만큼 edge 사이 Non-Negative weight 조건이 필요하다.
O(N^2 * log(N)) 으로 Spare인 경우 조금 더 낫다.

'SW 만학도 > C++ & Algorithm' 카테고리의 다른 글
| SSSP(Single Source Shortest Path) / APSP(All-Pairs Shortest Path) 실습 (0) | 2025.02.14 |
|---|---|
| C++ function implementation(feat, priority queue & DP) (0) | 2025.02.14 |
| Type Casting & Exception Handling + OOP 실습 (0) | 2025.02.12 |
| VS code C++ Debugging & Operator overloading (0) | 2025.02.03 |
| Function Overloading and Templates (0) | 2025.02.01 |