There exist two undirected trees with n and m nodes, numbered from 0 to n - 1 and from 0 to m - 1, respectively. You are given two 2D integer arrays edges1 and edges2 of lengths n - 1 and m - 1, respectively, where edges1[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the first tree and edges2[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the second tree.
You must connect one node from the first tree with another node from the second tree with an edge.
Return the minimum possible diameter of the resulting tree.
The diameter of a tree is the length of the longest path between any two nodes in the tree.
Example 1:

Input: edges1 = [[0,1],[0,2],[0,3]], edges2 = [[0,1]]
Output: 3
Explanation:
We can obtain a tree of diameter 3 by connecting node 0 from the first tree with any node from the second tree.
Example 2:
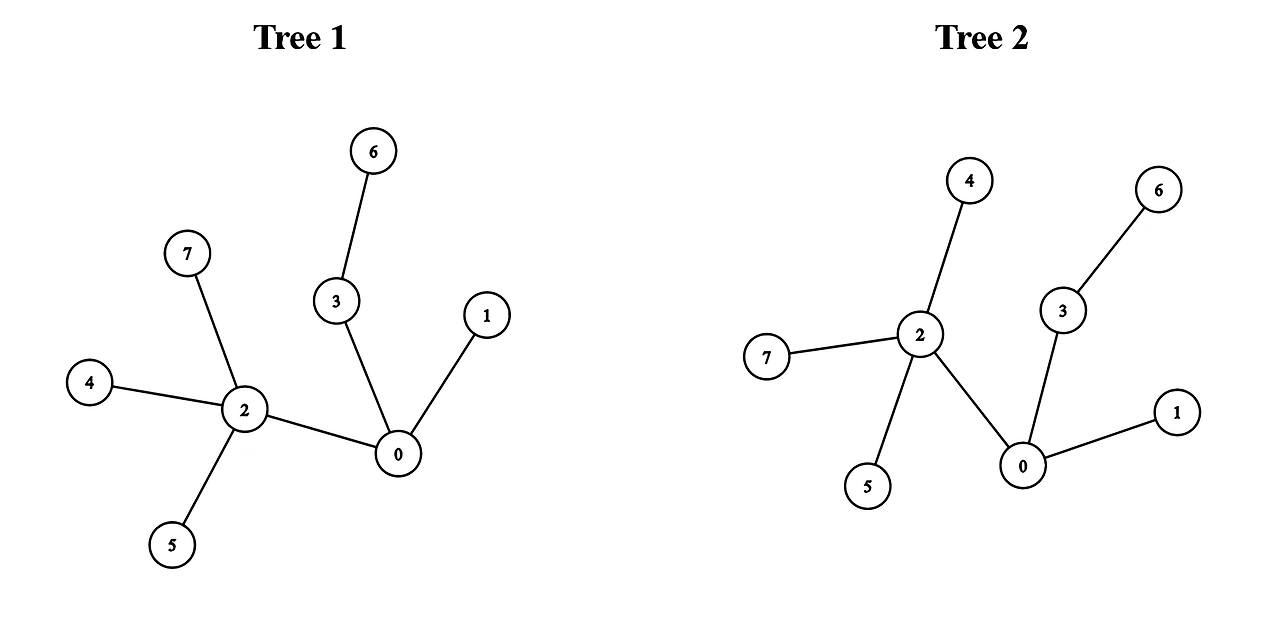
Input: edges1 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]], edges2 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]]
Output: 5
Explanation:
We can obtain a tree of diameter 5 by connecting node 0 from the first tree with node 0 from the second tree.
Constraints:
- 1 <= n, m <= 105
- edges1.length == n - 1
- edges2.length == m - 1
- edges1[i].length == edges2[i].length == 2
- edges1[i] = [ai, bi]
- 0 <= ai, bi < n
- edges2[i] = [ui, vi]
- 0 <= ui, vi < m
- The input is generated such that edges1 and edges2 represent valid trees.
일단, 문제부터 무지막지하게 길고 어려워 보인다. -_-;;;
Hard 난이도긴 하지만, 그래도 가야 할 길이기에 문제 Solve에 참여해본다..!
Graph에서 DFS를 구현하는 것이 목표이다..
Hint를 좀 보긴했지만 그래도 내 힘으로 잘 구현해냈다.
그러나 어김없이 찾아오는 Time limit의 한계 -_- 아오....
1. Python
솔직히 time limit까지 신경쓸 실력은 없는데 ㅠㅠ
class Solution:
def minimumDiameterAfterMerge(self, edges1: List[List[int]], edges2: List[List[int]]) -> int:
# They are not trees, graphs..
# Calculate DFS in edges1 and edges2, Result : DFS1(max 中 min) + DFS2(max 中 min) + 1
edges1 = sorted(edges1)
edges2 = sorted(edges2)
dfs1 = []
dfs2 = []
# How to solve it by recursion
def dfs(node:int,edge:list,visited:list) -> int:
ans = 0
for x in edge:
if node in x and x not in visited:
visited.append(x)
temp = x.copy() # Delete current node
temp.remove(node)
ans = max(ans, 1 + dfs(temp[0],edge,visited))
# ans = 1+dfs(temp[0],edge,visited)
return ans
for node in range(len(edges1)+1):
visited = []
dfs1.append(dfs(node,edges1,visited))
for node in range(len(edges2)+1):
visited = []
dfs2.append(dfs(node,edges2,visited))
return max(max(dfs1),max(dfs2),min(dfs1)+min(dfs2)+1)
GPT 말로는, 내 코드도 답 도출은 가능한데 시간 효율이 개똥이라고 한다-_-
기존 코드의 문제점 분석기존 코드에서 답 도출은 가능합니다. 하지만 다음과 같은 비효율적인 부분이 있습니다:
개선 후 코드의 장점
|
개선 코드 및 모범답안(?)은 아래와 같다.
class Solution:
def minimumDiameterAfterMerge(self, edges1: List[List[int]], edges2: List[List[int]]) -> int:
def build_adj_list(edges, n):
"""간선을 인접 리스트로 변환"""
adj = [[] for _ in range(n)]
for u, v in edges:
adj[u].append(v)
adj[v].append(u)
return adj
def dfs(node, adj, visited):
"""DFS를 통해 가장 먼 거리와 해당 노드 반환"""
visited[node] = True
max_depth = 0
farthest_node = node
for neighbor in adj[node]:
if not visited[neighbor]:
depth, farthest = dfs(neighbor, adj, visited)
if depth + 1 > max_depth:
max_depth = depth + 1
farthest_node = farthest
return max_depth, farthest_node
def find_diameter(edges):
"""트리의 직경 계산"""
n = len(edges) + 1
adj = build_adj_list(edges, n)
visited = [False] * n
_, farthest = dfs(0, adj, visited) # 임의의 노드에서 가장 먼 노드 찾기
visited = [False] * n
diameter, _ = dfs(farthest, adj, visited) # 가장 먼 노드에서 다시 DFS
return diameter
# 두 트리의 직경 계산
diameter1 = find_diameter(edges1)
diameter2 = find_diameter(edges2)
# 최소 직경 계산
return max(diameter1, diameter2, (diameter1 + 1) // 2 + (diameter2 + 1) // 2 + 1)
모범답안..
후덜덜하다. 특이하게 BFS를 썼네
class Solution:
def minimumDiameterAfterMerge(self, edges1: List[List[int]], edges2: List[List[int]]) -> int:
from collections import deque
def bfs_farthest(start, adj, n):
"""BFS를 통해 start 노드에서 가장 먼 노드와 거리를 반환"""
visited = [-1] * n
visited[start] = 0
queue = deque([start])
farthest_node = start
while queue:
node = queue.popleft()
for neighbor in adj[node]:
if visited[neighbor] == -1: # 방문하지 않은 경우
visited[neighbor] = visited[node] + 1
queue.append(neighbor)
farthest_node = neighbor
return farthest_node, visited[farthest_node]
def calculate_diameter(edges):
"""BFS를 두 번 실행하여 트리의 직경 계산"""
n = len(edges) + 1 # 노드 개수
adj = [[] for _ in range(n)]
for u, v in edges:
adj[u].append(v)
adj[v].append(u)
# BFS 1: 임의의 노드(0)에서 가장 먼 노드 찾기
farthest_node, _ = bfs_farthest(0, adj, n)
# BFS 2: 해당 노드에서 가장 먼 거리 계산
_, diameter = bfs_farthest(farthest_node, adj, n)
return diameter
# 각 트리의 직경 계산
diameter1 = calculate_diameter(edges1)
diameter2 = calculate_diameter(edges2)
# 병합 후 최소 직경 계산
radius1 = (diameter1 + 1) // 2
radius2 = (diameter2 + 1) // 2
return max(diameter1, diameter2, radius1 + radius2 + 1)
코드 설명
시간 복잡도
|
위 내용을 복습해서 C++로도 함 해봐야겠다.
솔직히 봐도 모르겄다 이거 아오;;
2. C++ 쉽지 않다...
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
class Solution {
public:
int minimumDiameterAfterMerge(vector<vector<int>>& edges1, vector<vector<int>>& edges2);
private:
int calculateDiameter(vector<vector<int>>& edges);
pair<int, int> bfs(int start, const vector<vector<int>>& adj, int n);
};
pair<int, int> Solution::bfs(int start, const vector<vector<int>>& adj, int n) {
vector<int> visited(n, -1);
queue<int> q;
q.push(start);
visited[start] = 0;
int farthest_node = start;
int max_distance = 0;
while (!q.empty()) {
int node = q.front();
q.pop();
for (int neighbor : adj[node]) {
if (visited[neighbor] == -1) {
visited[neighbor] = visited[node] + 1;
q.push(neighbor);
if (visited[neighbor] > max_distance) {
max_distance = visited[neighbor];
farthest_node = neighbor;
}
}
}
}
return {farthest_node, max_distance};
}
int Solution::calculateDiameter(vector<vector<int>>& edges) {
int n = edges.size() + 1;
vector<vector<int>> adj(n);
for (auto& edge : edges) {
adj[edge[0]].push_back(edge[1]);
adj[edge[1]].push_back(edge[0]);
}
// BFS 두 번으로 직경 계산
auto [farthest_node, _] = bfs(0, adj, n);
auto [_, diameter] = bfs(farthest_node, adj, n);
return diameter;
}
int Solution::minimumDiameterAfterMerge(vector<vector<int>>& edges1, vector<vector<int>>& edges2) {
int diameter1 = calculateDiameter(edges1);
int diameter2 = calculateDiameter(edges2);
int radius1 = (diameter1 + 1) / 2;
int radius2 = (diameter2 + 1) / 2;
return max({diameter1, diameter2, radius1 + radius2 + 1});
}