You are given the root of a binary tree with unique values.
In one operation, you can choose any two nodes at the same level and swap their values.
Return the minimum number of operations needed to make the values at each level sorted in a strictly increasing order.
The level of a node is the number of edges along the path between it and the root node.
Example 1:
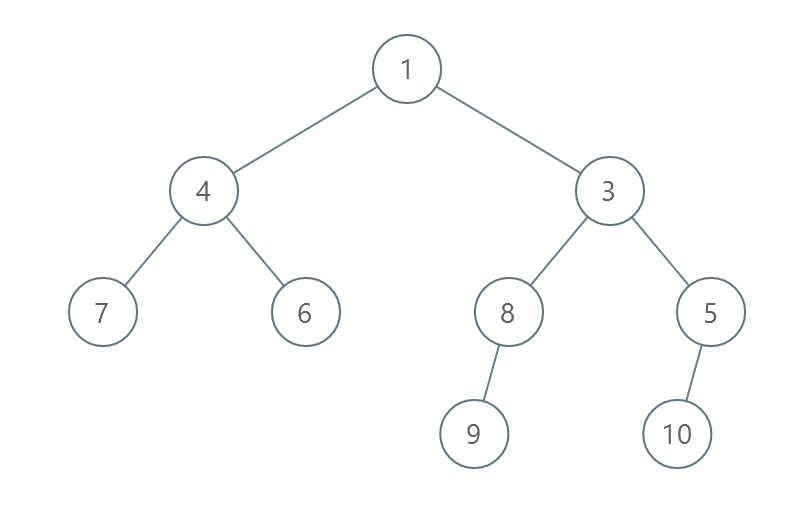
Input: root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
Output: 3
Explanation:
- Swap 4 and 3. The 2nd level becomes [3,4].
- Swap 7 and 5. The 3rd level becomes [5,6,8,7].
- Swap 8 and 7. The 3rd level becomes [5,6,7,8].
We used 3 operations so return 3.
It can be proven that 3 is the minimum number of operations needed.
Example 2:
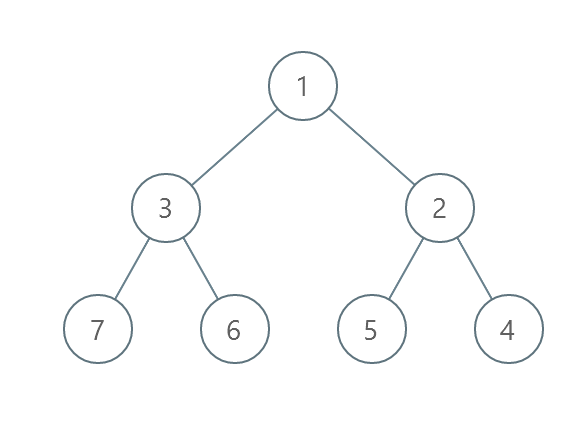
Input: root = [1,3,2,7,6,5,4]
Output: 3
Explanation:
- Swap 3 and 2. The 2nd level becomes [2,3].
- Swap 7 and 4. The 3rd level becomes [4,6,5,7].
- Swap 6 and 5. The 3rd level becomes [4,5,6,7].
We used 3 operations so return 3.
It can be proven that 3 is the minimum number of operations needed.
Example 3:
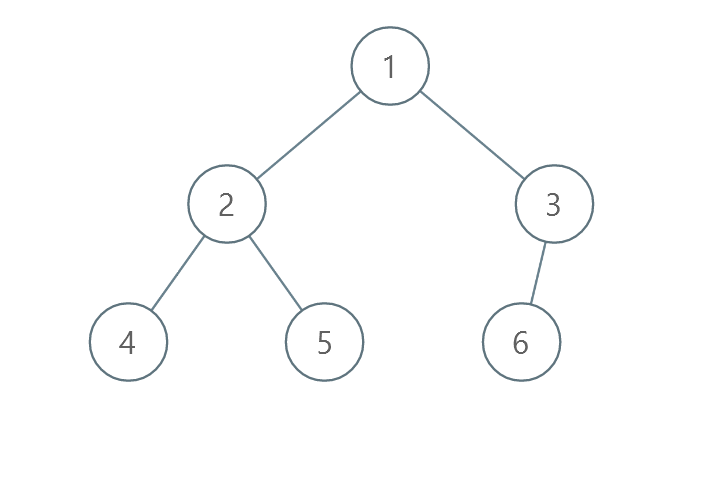
Input: root = [1,2,3,4,5,6]
Output: 0
Explanation: Each level is already sorted in increasing order so return 0.
Constraints:
- The number of nodes in the tree is in the range [1, 105].
- 1 <= Node.val <= 105
- All the values of the tree are unique.
이런 문제를 슬 연습할 때가 되었다.
각종 Node를 후리고 다니는 Tree문제! 함 들어가보자
이런거는 참고로 Python, C, C++ 모두 제약없이 쓸 수 있어야한다.
1. Python
내 풀이.. 역시나 Naive하긴 하다. 이런 경우에도 heap을 쓸 수 있을까? 일단 Pass는 했다만 역시 성능은 끝자락 ㅋ
아마 BFT는 괜찮은데 Level별로 Sorting하는 부분이 좀 짜칠 수도 있겠다.
Sorting Count하는 부분을 Method로 따로 뺐어야 했나?
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minimumOperations(self, root: Optional[TreeNode]) -> int:
ans = 0
if not root : return ans
from collections import deque
q = deque([root])
while q :
n = len(q)
temp_lv = []
for i in range(n):
curr = q.popleft()
if curr.left : q.append(curr.left)
if curr.right : q.append(curr.right)
temp_lv.append(curr.val)
temp_lv_sort = sorted(temp_lv)
for j in range(len(temp_lv)):
if temp_lv == temp_lv_sort : break
if temp_lv[j] == temp_lv_sort[j] : continue
else :
val = temp_lv_sort[j]
idx = temp_lv.index(val)
temp_lv[j],temp_lv[idx] = temp_lv[idx],temp_lv[j]
ans+=1
return ans
Python 모범답안도 함 체크해보자
아래와 같이 풀면 내 코드보다 시간효율이 10배 가량 좋다;;
class Solution:
def minimumOperations(self, root: Optional[TreeNode]) -> int:
q = deque([root])
ans = 0
while q:
a = []
for _ in range(len(q)):
node = q.popleft()
a.append(node.val)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
n = len(a)
a = sorted(range(n), key = lambda i: a[i])
vis = [False] * n
ans += n
for v in a:
if vis[v]:
continue
while not vis[v]:
vis[v] = True
v = a[v]
ans -= 1
return ans
사이클 분리 알고리즘이라는데, O(NlogM)의 효율을 자랑하지만 이해하기가 너무 어렵다 -_-
2. C
C문제는 공부도 할 겸 queue type을 직접 만들어보고 이를 활용해서 문제를 풀어보자
# C는 queue까지 모두 한 번에 정의의
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
// 큐 정의
typedef struct Queue {
struct TreeNode** data;
int front;
int rear;
int capacity;
} Queue;
// 큐 초기화
Queue* createQueue(int capacity) {
Queue* queue = (Queue*)malloc(sizeof(Queue));
queue->data = (struct TreeNode**)malloc(capacity * sizeof(struct TreeNode*));
queue->front = 0;
queue->rear = 0;
queue->capacity = capacity;
return queue;
}
// 큐 삽입
void enqueue(Queue* queue, struct TreeNode* node) {
queue->data[queue->rear++] = node;
}
// 큐 제거
struct TreeNode* dequeue(Queue* queue) {
return queue->data[queue->front++];
}
// 큐가 비었는지 확인
bool isEmpty(Queue* queue) {
return queue->front == queue->rear;
}
// 정렬 비교 함수
int compare(const void* a, const void* b) {
return (*(int*)a - *(int*)b);
}
// 최소 스왑 계산
int calculateSwaps(int* arr, int n) {
int swaps = 0;
// 정렬된 배열 생성
int* sorted = (int*)malloc(n * sizeof(int));
for (int i = 0; i < n; i++) {
sorted[i] = arr[i];
}
qsort(sorted, n, sizeof(int), compare);
// 현재 배열을 정렬된 배열로 맞추기 위해 스왑 계산
for (int i = 0; i < n; i++) {
while (arr[i] != sorted[i]) {
// arr[i]의 값을 정렬된 위치로 이동
int targetIndex = -1;
for (int j = 0; j < n; j++) {
if (arr[j] == sorted[i]) {
targetIndex = j;
break;
}
}
// 스왑
int temp = arr[i];
arr[i] = arr[targetIndex];
arr[targetIndex] = temp;
swaps++;
}
}
free(sorted);
return swaps;
}
// 트리의 최소 작업 계산
int minimumOperations(struct TreeNode* root) {
if (!root) return 0;
int ans = 0;
Queue* queue = createQueue(100000); // 충분한 크기의 큐 생성
enqueue(queue, root);
while (!isEmpty(queue)) {
int level_size = queue->rear - queue->front; // 현재 레벨의 노드 수
int* level = (int*)malloc(level_size * sizeof(int));
int idx = 0;
// 현재 레벨 순회
for (int i = 0; i < level_size; i++) {
struct TreeNode* node = dequeue(queue);
level[idx++] = node->val;
if (node->left) {
enqueue(queue, node->left);
}
if (node->right) {
enqueue(queue, node->right);
}
}
// 현재 레벨에서 최소 스왑 계산
ans += calculateSwaps(level, level_size);
free(level);
}
// 큐 메모리 해제
free(queue->data);
free(queue);
return ans;
}
3. C++
C++ 노가다로 파이썬이랑 똑같은 logic으로 풀었다.
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minimumOperations(TreeNode* root) {
int ans = 0;
queue<TreeNode*> q;
if(!root) return ans;
q.push(root);
while(!q.empty()){
int n = q.size();
vector<int> vec;
for(int i=0;i<n;i++){
TreeNode* curr = q.front();
q.pop();
vec.push_back(curr->val);
if(curr->left) q.push(curr->left);
if(curr->right) q.push(curr->right);
}
vector<int> origin = vec;
sort(vec.begin(),vec.end());
for(int j=0;j<vec.size();j++){
if(vec==origin) break;
if(vec[j]==origin[j]) continue;
else{
int val = origin[j];
int idx = -1;
for(int k=j+1;k<vec.size();k++){
if(vec[k]==val){
idx = k;
break;
}
}
swap(vec[idx],vec[j]);
ans++;
}
}
}
return ans;
}
};
좀 더 효율적인 답지는 아래와 같고
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minimumOperations(TreeNode* root) {
queue<TreeNode*> q;
q.push(root);
int swaps=0;
while(!q.empty()){
int qz=q.size();
vector<int> idx(qz, 0);
iota(idx.begin(), idx.end(), 0);
vector<int> arr(qz, 0);
for(int i=0; i<qz; i++){
auto node=q.front();
q.pop();
arr[i]=node->val;
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
// each value is unique, no need for stable_sort
sort(idx.begin(), idx.end(), [&](int i, int j){
return arr[i]<arr[j];
});
for(int i=0; i<qz; ){
int j=idx[i];
if (j!=i){// recheck
swaps++;
swap(idx[i], idx[j]);
}
else i++; // next iteration
}
}
return swaps;
}
};
이게 젤 나은듯
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minSwaps(vector<int>& arr) {
vector<pair<int,int>>v;
for(int i=0; i<arr.size(); i++){
v.push_back({arr[i],i}); // {value,index}
}
sort(v.begin(), v.end());
int swaps = 0;
for(int i=0; i<arr.size(); i++){
pair<int,int>p = v[i];
int index = p.second;
while(i != index){
swaps++;
swap(v[i], v[index]);
index = v[i].second;
}
}
return swaps;
}
int minimumOperations(TreeNode* root) {
queue<TreeNode*>qu;
qu.push(root);
int ans = 0;
vector<int>levelOrder;
while(!qu.empty()){
levelOrder.clear();
int n = qu.size();
for(int i=0; i<n; i++){
TreeNode* temp = qu.front();
qu.pop();
levelOrder.push_back(temp->val);
if(temp->left) qu.push(temp->left);
if(temp->right) qu.push(temp->right);
}
int minimumSwaps = minSwaps(levelOrder);
ans += minimumSwaps;
}
return ans;
}
};