Given the root of a binary tree, return the postorder traversal of its nodes' values.
Example 1:
Input: root = [1,null,2,3]
Output: [3,2,1]
Explanation:

Example 2:
Input: root = [1,2,3,4,5,null,8,null,null,6,7,9]
Output: [4,6,7,5,2,9,8,3,1]
Explanation:

Example 3:
Input: root = []
Output: []
Example 4:
Input: root = [1]
Output: [1]
Constraints:
- The number of the nodes in the tree is in the range [0, 100].
- -100 <= Node.val <= 100
Follow up: Recursive solution is trivial, could you do it iteratively?
이왕 Binary Tree 톺아볼때, 모든 Traversal 다 한 번씩 복습해보기 + 다양한 방법을 다 이용해보기
- Post-order
1. Python
# Python Post-order - Iterative
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root : return []
s = deque()
s.append(root)
visited = []
while s:
curr = s.pop()
visited.append(curr.val)
if curr.left :
s.append(curr.left)
if curr.right:
s.append(curr.right)
return visited[::-1]# postorder with Recursive
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
ans = []
if not root : return ans
def dfs(node):
if not node : return
dfs(node.left)
dfs(node.right)
ans.append(node.val)
dfs(root)
return ans
2. Post Order C, recursive
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* postorderTraversal(struct TreeNode* root, int* returnSize) {
if(!root){
*returnSize = 0;
return NULL;}
int* ans = (int*)malloc(100*sizeof(int));
int cnt = 0;
dft_help(root,ans,&cnt);
*returnSize = cnt;
return ans;
}
void dft_help(struct TreeNode* node,int* ans,int* cnt){
if(!node) return;
dft_help(node->left,ans,cnt);
dft_help(node->right,ans,cnt);
ans[(*cnt)++] = node->val;
}
3. Post Order C++, Recursive
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ans; // new?
if(!root) return ans;
dft_help(root,&ans);
return ans;
}
void dft_help(TreeNode* node,vector<int>* ans){
if(!node) return;
dft_help(node->left,ans);
dft_help(node->right,ans);
ans->push_back(node->val);
}
};/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ans; // new?
if(!root) return ans;
dft_help(root,ans);
return ans;
}
void dft_help(TreeNode* node,vector<int>& ans){
if(!node) return;
dft_help(node->left,ans);
dft_help(node->right,ans);
ans.push_back(node->val);
}
};
4. Post Order C++ iterative하게 푸는 건데.. 오바다 with 1 stack
#include <vector>
#include <stack>
using namespace std;
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
if (!root) return result;
stack<TreeNode*> s;
TreeNode* lastVisited = nullptr;
TreeNode* current = root;
while (!s.empty() || current) {
if (current) {
s.push(current);
current = current->left; // 왼쪽 자식으로 계속 이동
} else {
TreeNode* node = s.top();
// 오른쪽 자식이 존재하고 아직 방문하지 않았다면
if (node->right && lastVisited != node->right) {
current = node->right;
} else {
result.push_back(node->val);
s.pop();
lastVisited = node;
}
}
}
return result;
}
};
5. Preorder
https://leetcode.com/problems/binary-tree-preorder-traversal/
Given the root of a binary tree, return the preorder traversal of its nodes' values.
Example 1:
Input: root = [1,null,2,3]
Output: [1,2,3]
Explanation:

Example 2:
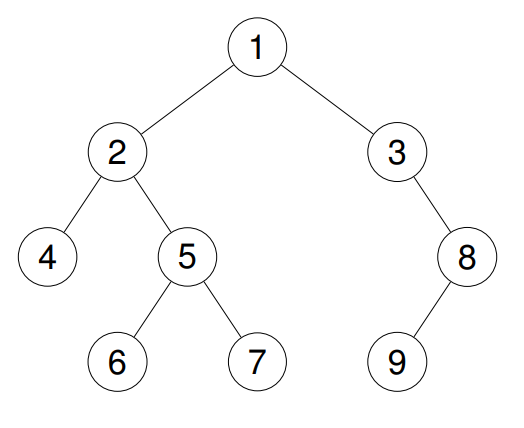
Input: root = [1,2,3,4,5,null,8,null,null,6,7,9]
Output: [1,2,4,5,6,7,3,8,9]
Explanation:
Example 3:
Input: root = []
Output: []
Example 4:
Input: root = [1]
Output: [1]
Constraints:
- The number of nodes in the tree is in the range [0, 100].
- -100 <= Node.val <= 100
Follow up: Recursive solution is trivial, could you do it iteratively?
6. Python Preorder Recursive
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root : return []
ans = []
def dft_help(node) :
if not node : return
ans.append(node.val)
dft_help(node.left)
dft_help(node.right)
dft_help(root)
return ans
7. Python Preorder Iterative
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root : return []
s = deque([root])
ans = []
while s :
curr = s.pop()
ans.append(curr.val)
if curr.right : s.append(curr.right)
if curr.left : s.append(curr.left)
return ans
8. C Preorder Recursive ( C는 container 만드는게 너무 짜쳐서 iterative말고 recursive만 ㄱㄱ)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
if(!root){
*returnSize = 0;
return NULL;
}
int* ans = (int*)malloc(100*sizeof(int));
int cnt = 0;
dft_help(root,ans,&cnt);
*returnSize = cnt;
return ans;
}
void dft_help(struct TreeNode* node, int* ans, int* cnt){
if(!node) return;
ans[(*cnt)++] = node->val;
dft_help(node->left,ans,cnt);
dft_help(node->right,ans,cnt);
}
9. C++ Preorder Iterative
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ans;
if(!root) return ans;
stack<TreeNode*> s;
s.push(root);
while(!s.empty()){
TreeNode* curr = s.top();
s.pop();
ans.push_back(curr->val);
if(curr->right) s.push(curr->right);
if(curr->left) s.push(curr->left);
}
return ans;
}
};
10. C++ preorder Recursive
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ans;
if(!root) return ans;
dft_help(root,ans);
return ans;
}
void dft_help(TreeNode* node, vector<int>& ans){
if(!node) return;
ans.push_back(node->val);
dft_help(node->left,ans);
dft_help(node->right,ans);
}
};
- Inorder Traversal
https://leetcode.com/problems/binary-tree-inorder-traversal/
Given the root of a binary tree, return the inorder traversal of its nodes' values.
Example 1:
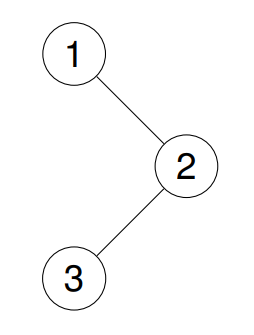
Input: root = [1,null,2,3]
Output: [1,3,2]
Explanation:
Example 2:
Input: root = [1,2,3,4,5,null,8,null,null,6,7,9]
Output: [4,2,6,5,7,1,3,9,8]
Explanation:

Example 3:
Input: root = []
Output: []
Example 4:
Input: root = [1]
Output: [1]
Constraints:
- The number of nodes in the tree is in the range [0, 100].
- -100 <= Node.val <= 100
Follow up: Recursive solution is trivial, could you do it iteratively?
11. Python Inorder Recursive
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
ans = []
if not root : return ans
def dfs_help(node):
if not node : return
dfs_help(node.left)
ans.append(node.val)
dfs_help(node.right)
dfs_help(root)
return ans
12. Python Inorder Iterative - 어렵다
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
ans = []
if not root : return ans
s = deque()
curr = root
while s or curr :
while curr:
s.append(curr)
curr = curr.left
curr = s.pop()
ans.append(curr.val)
curr = curr.right
return ans
13. C Inorder Recursive
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* inorderTraversal(struct TreeNode* root, int* returnSize) {
if(!root){
*returnSize = 0;
return NULL;
}
int* ans = (int*)malloc(100*sizeof(int));
int cnt = 0;
dfs_help(root,ans,&cnt);
*returnSize = cnt;
return ans;
}
void dfs_help(struct TreeNode* node, int* ans, int* cnt){
if(!node) return;
dfs_help(node->left,ans,cnt);
ans[(*cnt)++] = node->val;
dfs_help(node->right,ans,cnt);
}
14. C++ Inorder Iterative
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> vec;
if(!root) return vec;
stack<TreeNode*> s;
TreeNode* curr = root;
while(!s.empty() || curr ){
while(curr){
s.push(curr);
curr = curr->left;
}
curr = s.top();
s.pop();
vec.push_back(curr->val);
curr = curr->right;
}
return vec;
}
};
15. C++ Inorder Recursive
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> vec;
if(!root) return vec;
dfs_help(root,vec);
return vec;
}
void dfs_help(TreeNode* node,vector<int> &vec){
if(!node) return;
dfs_help(node->left,vec);
vec.push_back(node->val);
dfs_help(node->right,vec);
}
};