12. Data Structures ( Stacks & Queues )
https://eglife.tistory.com/30 11. Data Structures ( Arrays & Linked Lists ) 본격적인 자료구조에 대한 공부! Python에서 list를 겁~나게 다뤘는데, 사실 이 List는 고마운 친구였다는 것이다. 그 고마운 List의 내부구조
eglife.tistory.com

슬 복잡해지는 자료구조
지금껏 배웠던 자료구조는 Linear하다면 이제는 non-Linear한 Case도 슬슬 나온다.
Tree의 정의

- Tree / Subtree의 Recursive한 구조이다.
- Node = Vertex = 꼭지
- Root : Paret가 없는 맨 위 Node , Leaf : Child가 없는 맨 아래 Node
Binary Tree
- 자식을 최대 둘까지만 가질 수 있는 Tree

- Base Case : Tree is Empty , - General Case : Tree가 자식 Node를 가질 수도 있고 안 가질 수도 있는데 가진다면 Max 2개이고 2개라면 반드시 Left / Right가 구분이 되어야 함
- Height of Tree : Root - Leaf 까지의 길이 중 Node 기준(edge 직선 기준 X) 최대값
Full Binary Tree
- Tree의 Height 를 h라고 했을 때 --> Tree가 비어 있거나(h=0) , h-1인 left / right subtree가 모두 full이어야 한다.
(대충 Height 0,1,2,3... 기준 채울 수 있는 모든 것들이꽉 차있으면 된다.)
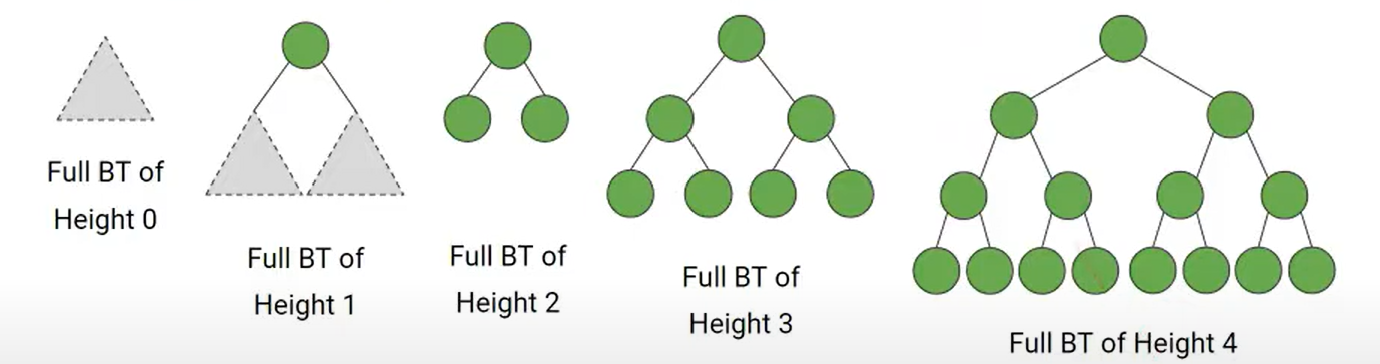
Complete Binary Tree ( Full과 이름이 비슷 ;; )
- h-1까지는 tree가 full로 차 있고, 마지막 h level (leaf 단) 에선 node가 full로 차 있어도 되고 차 있지 않아도 된다. 다만, 차 있다면 왼쪽부터 채운다. --> 뭔가 억지스러운 정의 -_-

Array - Based Implementation
- Array : 연속적이고 처음부터 그 길이를 알고 있는 메모리공간
( 장점 : Random access가 가능하다. 아무곳이나 찍고 이 index의 값을 달라! 해도 바로 O(1)로 Return 해준다.)

- Parent 와 Child Index 사이의 관계는 위와 같다.
- 그러나 위 그림처럼 빈 공간이 많으면 Memory 효율이 떨어진다. Height가 늘어날 수록 자리만 차지하는 빈 공간이 커지는 것이니! --> Linked List로 구현을 하자
Reference - based Implementation
class treenode():
def __init__(self,x):
self.item = x
self.left = None
self.right = None
class binary_tree():
def __init(self,node):
self.root = node
Tree Traversal
- Node를 순회하며 Data를 읽는다.
- 그 순서에 따라 구분 有
1. Preorder : Root -> Left Subtree -> Right Subtree [ ROOT 먼저, 그리고 좌-우순 ]
2. Inorder : Left Subtree -> Root -> Right Subtree
3. Postorder : Left Subtree -> Right Subtree -> Root [ ROOT 꼴등, 그 전에 좌-우순]

- Traversal 예시

- 어떤 Tree가 주어져도, Preorder / Inorder / Postorder Traversal에 따라 Node 방문 순서를 표현할 수 있어야한다.
Tree Traversal Implementation
- Use Recursion !!!
- Base Case : Empty tree를 방문하면 do nothing
- General Case : 2개의 Recursive call 을 해주고, Root를 Visit!
- Traversal 종류 ( pre/in/post )에 따라 순서만 조정해주면 된다.
def preorder(node):
if node is not None:
print(node.item)
preorder(node.left)
preorder(node.right)
# preorder(root)
def inorder(node):
if node is not None:
inorder(node.left)
print(node.item)
inorder(right.left)
# inorder(root)
def postorder(node):
if node is not None:
postorder(node.left)
postorder(node.right)
print(node.item)
# postorder(root)
Binaey Search Tree
- 자료구조 활용을 위한 '진짜' Tree 구조 ㅎㅎ.. ( Key(node) / Item(value) 로 이루어진..)
- Data를 읽고 삭제하고 수정하기 위함 ( Insert / Retrieve(search) / Delete) while Binary Search 구조를 지키면서!
- Binary Search Tree의 특성
- Root를 기준으로 모든 LV에서 Left Subtree는 Root보다 작고, Right Subtree는 Root보다 커야 한다.
- 중복 값은 X
Retrieval ( Search )

- Recursive 냄가 솔솔 난다.
def search(root, key):
if root is None:
return None # CAN'T FIND
elif key == root.item():
return root # Find it
elif key > root.item():
search(root.right,key)
else :
search(root.left,key)
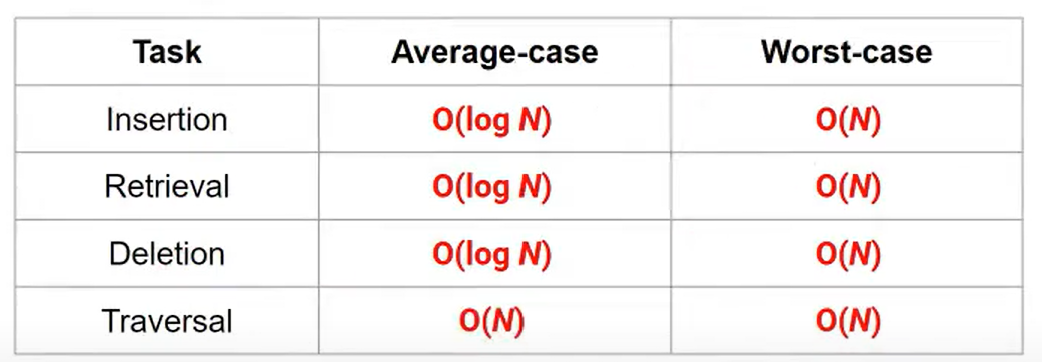
Retrieval Time Complexity
- 한 Iteration에서 Calculation 의 Time Complexity --> 값 비교, 어느 방향으로 Search 할 지 결정 --> N(1)
- Worst Case에선 Tree 의 Height만큼 Calculate을 진행한다.

- Tree의 Height은 그 모양에 따라 다르다. Balanced 일 때는 Height --> O(log N) 이고, Unbalanced --> O(N)
Insertion
- 일단 기본적으로 위 Retrieval ( Search ) 구조를 따라간다.
- Why? 일단, 값의 중복이 있으면 안 되니까 Search에서 Fiind it! 했던 부분이 나오면 Error를 Return 하고, 그게 아니고 Search에서 fail 했다면 그 값이 있어야 할 곳을 일단 찾은거니까 그 부분에 넣고자 하는 Value를 put 한다.
def insert(root,x):
if root is None:
new_node = treenode(x)
return new_node # Base Case
elif x == root.item():
print("Error")
return None
elif x < root.item():
new_subtree = insert(root.left,x)
root.left = new_subtree
return root
else: # x > root.item()
new_subtree = insert(root.right,x)
root.right = new_subtree
return root
Deletion
- 삭제가 어려운 이유 ... 삭제가 되어도 BST(Binary Search Tree) 구조가 유지되어야 한다 ㅠㅠ
1) Leaf을 삭제하는 경우 --> 쉽다. 그냥 삭제 때리면 된다.
2) Single child를 갖는 Node를 삭제하는 경우 --> 삭제 후 subtree를 그대로 붙힌다.
3) Double child를 갖는 Node를 삭제하는 경우 --> 왼쪽 subtree의 rightmost 또는 오른쪽 subtree의 leftmost를 new root로!
- Case 1 / 2 는 쉽다. 3이 문제!!
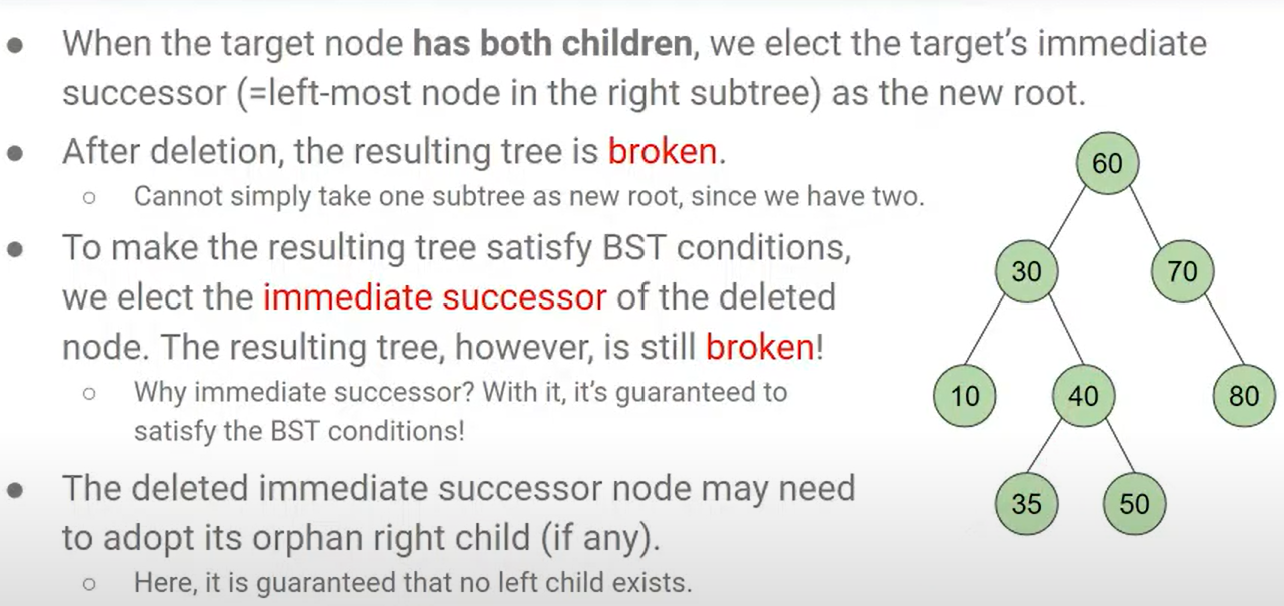
def delete(root,x):
if root is None:
return None
elif x < root.item() :
root.left = delete(root.left,x)
elif x > root.item() :
root.right = delete(root.right,x)
else: # 지우려는 대상에 도달을 했다.
if root.left is None:
new_root = root.right
root = None #원래 있던 root는 삭제
return new_root
elif root.right is None:
new_root = root.left
root = None
return new_root #요까지 하면 자식 0,1명은 clear
else: # 자식이 둘 다 있는 경우...!
im_su = get_immediate_successor(root)
root.item() = im_su.item() # im_su의 값만 딱 복사
root.right = delete(root.right,im_sum.item())
#right side에서 left most인 값을 찾았기에 2 children인 경우가 나오지 않는다.
# Base한 케이스에서 딱 삭제되는 운명임.
def get_immediate_successor(target):
curr = target.right
while curr.left is not None:
curr = curr.left #left로 쭉 끝까지 간다.
return curr # right subtree의 leftmost = immediate successor--> Code Error가 있을 수도 있다. 재확인 필요
Shape of Tree
- Tree의 모양은 Data의 Insertion 순서에 따라 모양이 달라진다.

Balanced Tree
- Red-black tree 알고리즘 : 최대 Height가 lon(N+1) 대비 2만큼만 낮게 만드는 알고리즘
- AVL Tree : 위 경우에서 최대 1만큼만 낮게 만드는 알고리
Tree sort
- Inorder traversal 로 하면 tree 내의 data sort가 가능하다.
- Time Complexity ?
- N개의 data를 Tree Height 구조에다가 넣어야 한다. --> Height * N

- 완벽한 Balanced tree이면 log N 높이에 한 번씩 방문하는 것 N 곱해서 O(NlogN), 그리고 출력 O(N) 즉, 총 O(NlogN)
--> Merge Sort와 같은 Time Complexity
- Worst Case --> Tree가 Linked List처럼 직선이라면 O(N^2) 이다.
BST 응용문제
- SW Engineer 문제에서 많이 언급되는 부분



- 위 모든 Tree 문제는 Recursive하게 풀 수 있다. Tree는 Recursive 그 잡채!!
- 3번 Q에대한 pseudo code

Tree 구조는 DATA 삽입 , 탐색, 삭제 모두 Time Complexity는 O(log N)이라 실제로 많이 쓰이는 자료구조이다.
많이 쓰이는만큼 관련된 문제도 잘 풀 줄 알아야겠다.

'SW 만학도 > Python' 카테고리의 다른 글
| Review 2 - Python의 기본 Module , Class (0) | 2024.07.01 |
|---|---|
| Review 1 - Python programming basics (1) | 2024.07.01 |
| 12. Data Structures ( Stacks & Queues ) (0) | 2024.03.25 |
| 11. Data Structures ( Arrays & Linked Lists ) (2) | 2024.03.18 |
| 10 - 1 . Recursion으로 Sort 코드 + Merge Sort 구현해보기 (0) | 2024.03.18 |