https://leetcode.com/problems/search-a-2d-matrix-ii/description/
Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example 1:
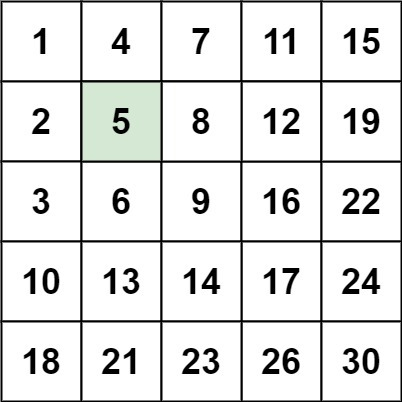
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true
Example 2:
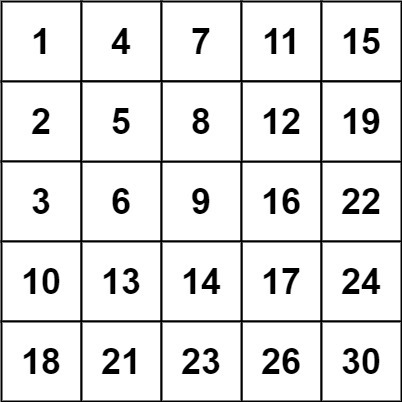
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false
Constraints:
- m == matrix.length
- n == matrix[i].length
- 1 <= n, m <= 300
- -109 <= matrix[i][j] <= 109
- All the integers in each row are sorted in ascending order.
- All the integers in each column are sorted in ascending order.
- -109 <= target <= 109
이번엔 째끔 익숙한 leetcode 문제인데,
달갑지만은 않다.
Matrix 문제라서..ㅠㅠㅠ
일단 한 번 도으전!
1.Python
풀어냈다. on my own..
근데 하다보니 느끼는 건, leetcode는 어떤 test case에서 어떻게 값이 잘못 나왔는지 알려주어서 debugging이 좀 편하다.
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
m = len(matrix)
n = len(matrix[0])
row_idx = 0
for i in range(m):
if matrix[i][0] >= target:
if matrix[i][0] == target : return True
break
else : row_idx += 1
if row_idx == -1 : return False
for j in range(row_idx): # index check!
# Binary Search for each row
left = 0
right = n-1
while left <= right:
mid = (left+right)//2
if matrix[j][mid] == target : return True
elif matrix[j][mid] > target : right = mid-1
else : left = mid+1
return False
꾸역승으로 기껏 binary search 썼더니만, 풀이는 예상 외로 간단허다..
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
if not matrix or not matrix[0]:
return False
m = len(matrix)
n = len(matrix[0])
# 시작은 왼쪽 아래에서 시작
row = m - 1
col = 0
while row >= 0 and col < n:
if matrix[row][col] == target:
return True
elif matrix[row][col] > target:
row -= 1 # 값을 줄여서 윗 행으로 이동
else:
col += 1 # 값을 키워서 오른쪽 열로 이동
return False
코드 보고도 이게 뭐여 .. error code인가? 했는데
알고보니 문제의 Matrix 특성을 십분 잘 활용한 코드였다..
2. C
bool searchMatrix(int** matrix, int matrixSize, int* matrixColSize, int target){
int m = matrixSize-1;
int n = *matrixColSize-1;
int col = 0;
while(m>=0 && col<=n){
if(matrix[m][col]==target) return true;
else if(matrix[m][col] < target) col++;
else m--;
}
return false;
}
사람이 무서운게, 한 번 편한 방법을 찾아버리면 거기에 적응을 해버린다.
C++은 다시 binary Search로 때려보기
3. C++
#include <vector>
using namespace std;
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size();
int n = matrix[0].size();
int idx = 0;
for(int i=0;i<m;i++){
if(matrix[i][0]>target) break;
idx++;
}
if(idx==0) return false;
for(int j=0;j<idx;j++){
int left = 0;
int right = n-1;
while(left<=right){
int mid = (left+right)/2;
if(matrix[j][mid]==target) return true;
else if(matrix[j][mid] < target) left = mid+1;
else right = mid-1;
}
}
return false;
}
};
오늘은 요기까지..!
'Coding_Practice' 카테고리의 다른 글
| TieRopes (0) | 2024.10.24 |
|---|---|
| Maximum Swap[Math,Greedy] (2) | 2024.10.17 |
| MinMaxDivision(Divide array A into K blocks and minimize the largest sum of any block) (1) | 2024.10.16 |
| MaxProductOfThree (0) | 2024.10.16 |
| Quick_Sort 문제 풀기(Divide and conquer) (1) | 2024.10.16 |